Sine
Sine, written as sin(θ), is one of the six fundamental trigonometric functions.
Sine definitions
There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. The right-angled triangle definition of trigonometric functions is most often how they are introduced, followed by their definitions in terms of the unit circle.
Right triangle definition
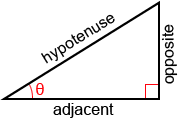
For a right triangle with an acute angle, θ, the sine value of this angle is defined to be the ratio of the opposite side length to the hypotenuse length.
The sides of the right triangle are referenced as follows:
- Adjacent: the side next to θ that is not the hypotenuse
- Opposite: the side opposite θ.
- Hypotenuse: the longest side of the triangle opposite the right angle.
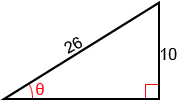
Example:
Find sin(θ) for the right triangle below.
We can also use the sine function when solving real world problems involving right triangles.
Example:
A wheel chair ramp needs to have an angle of 10° and a rise of 3 feet, what is the length of the ramp?

Unit circle definition
Trigonometric functions can also be defined as coordinate values on a unit circle. A unit circle is a circle of radius 1 centered at the origin. The right triangle definition of trigonometric functions allows for angles between 0° and 90° (0 and in radians). The unit circle definition allows us to extend the domain of trigonometric functions to all real numbers. Refer to the figure below.
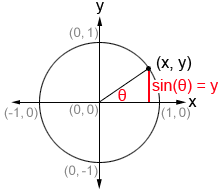
Given a point (x, y) on the circumference of the unit circle, we can form a right triangle, as shown in the figure. In such a triangle, the hypotenuse is the radius of the unit circle, or 1. θ is the angle formed between the initial side of an angle along the x-axis and the terminal side of the angle formed by rotating the ray either clockwise or counterclockwise. The terminal side of the angle is the hypotenuse of the right triangle and is the radius of the unit circle. Therefore, it always has a length of 1. Thus, we can use the right triangle definition of sine to determine that
meaning that the y-value of any point on the circumference of the unit circle is equal to sin(θ).
Unlike the definitions of trigonometric functions based on right triangles, this definition works for any angle, not just acute angles of right triangles, as long as it is within the domain of sin(θ). The domain of the sine function is (-∞,∞) and its range is [-1,1].
sin values
There are many methods that can be used to determine the value for sine, such as referencing a table of cosines, using a calculator, and approximating using the Taylor Series of sine. In most practical cases, it is not necessary to compute a sine value by hand, and a table, calculator, or some other reference will be provided.
Sine calculator
The following is a calculator to find out either the sine value of an angle or the angle from the sine value. If you are looking for a sin-1 calculator, refer to the arcsin page.
Commonly used angles
While we can find sine value for any angle, there are some angles that are more frequently used in trigonometry. Below are 16 commonly used angles in both radians and degrees, along with the coordinates of their corresponding points on the unit circle.
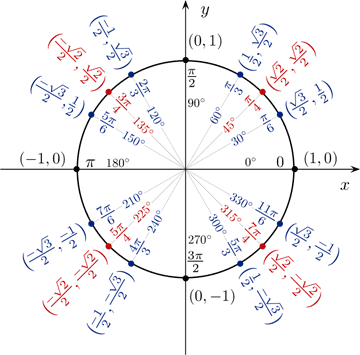
The above figure serves as a reference for quickly determining the sines (y-value) and cosines (x-value) of angles that are commonly used in trigonometry. As can be seen from the figure, sine has a value of 0 at 0° and a value of 1 at 90°. Cosine follows the opposite pattern; this is because sine and cosine are cofunctions (described later). The other commonly used angles are 30° (), 45° (
), 60° (
) and their respective multiples. The cosine and sine values of these angles are worth memorizing in the context of trigonometry, since they are very commonly used.
One method that may help with memorizing these values is to express all the values of sin(θ) as fractions involving a square root. Starting from 0° and progressing through 90°, sin(0°) = 0 = . The subsequent values, sin(30°), sin(45°), sin(60°), and sin(90°) follow a pattern such that, using the value of sin(0°) as a reference, to find the values of sine for the subsequent angles, we simply increase the number under the radical sign in the numerator by 1, as shown below.
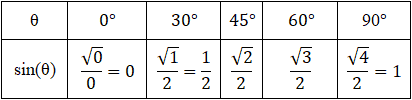
The values of sine from 0° through -90° follow the same pattern except that the values are negative instead of positive since sine is negative in quadrant IV. This pattern repeats periodically for the respective angle measurements, and we can identify the values of sin(θ) based on the position of θ in the unit circle, taking the sign of sine into consideration: sine is positive in quadrants I and II and negative in quadrants III and IV. A similar memorization method can be used for cosine. Refer to the cosine page if necessary.
Knowing the values of cosine and sine for angles in the first quadrant allows us to determine their values for corresponding angles in the rest of the quadrants in the coordinate plane through the use of reference angles.
Reference angles
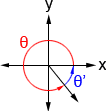
A reference angle is an acute angle (<90°) that can be used to represent an angle of any measure. Any angle in the coordinate plane has a reference angle that is between 0° and 90°. It is always the smallest angle (with reference to the x-axis) that can be made from the terminal side of an angle. The figure below shows an angle θ and its reference angle θ'.
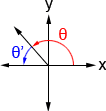
Because θ' is the reference angle of θ, both sin(θ) and sin(θ') have the same value. For example, 30° is the reference angle of 210°, and if we reference the unit circle, we can see that the sine values of both have a magnitude of 1/2, albeit they have different signs. Because all angles have a reference angle, we really only need to know the values of sin(θ) (as well as those of other trigonometric functions) in quadrant I. All other corresponding angles will have values of the same magnitude, and we just need to pay attention to their signs based on the quadrant that the terminal side of the angle lies in. Below is a table showing the signs of cosine, sine, and tangent in each quadrant.
| Sine | Cosine | Tangent | |
| Quadrant I | + | + | + |
| Quadrant II | + | - | - |
| Quadrant III | - | - | + |
| Quadrant IV | - | + | - |
Once we determine the reference angle, we can determine the value of the trigonometric functions in any of the other quadrants by applying the appropriate sign to their value for the reference angle. The following steps can be used to find the reference angle of a given angle, θ:
- Subtract 360° or 2π from the angle as many times as necessary (the angle needs to be between 0° and 360°, or 0 and 2π). If the resulting angle is between 0° and 90°, this is the reference angle.
- Determine what quadrant the terminal side of the angle lies in (the initial side of the angle is along the positive x-axis)
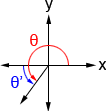
- Depending what quadrant the terminal side of the angle lies in, use the equations in the table below to find the reference angle. In quadrant I, θ'=θ.
| Quadrant II | Quadrant III | Quadrant IV |
|---|---|---|
 |
 |
 |
| θ'= 180° - θ | θ'= θ - 180° | θ'= 360° - θ |
Example:
Find sin(120°).
- θ is already between 0° and 360°
- 120° lies in quadrant II
- 180° - 120° = 60°, so the reference angle is 60°
sin(60°)=. 120° is in quadrant II, and sine is positive in quadrant II, so:
Example:
Find sin(690°).
- 690° - 360° = 330°
- 330° lies in quadrant IV
- 360° - 330° = 30°, so the reference angle is 30°
sin(30°)=. 330° is in quadrant IV where sine is negative, so:
Properties of the sine function
Below are a number of properties of the sine function that may be helpful to know when working with trigonometric functions.
Sine is a cofunction of cosine
A cofunction is a function in which f(A) = g(B) given that A and B are complementary angles. In the context of cosine and sine,
sin(θ) = cos(90° - θ)
cos(θ) = sin(90° - θ)
Example:
sin(60°) = cos(90° - 60°) = cos(30°)
Referencing the unit circle shown above, we can plug in values for cos(30°) and sin(60°) and see that:
Sine is an odd function
An odd function is a function in which -f(x)=f(-x). It has symmetry about the origin. Thus,
-sin(θ) = sin(-θ)
Example:
| -sin(60°) = sin(-60°) |
| -sin(60°) = sin(300°) |
Referencing the unit circle, we can see that sin(60°)=, so -sin(60°)=
, and sin(-60°) is equivalent to sin(-60° + 360°) = sin(300°), which is equal to
. This is only one example, but this property holds true for all angles.
Sine is a periodic function
A periodic function is a function, f, in which some positive value, p, exists such that
f(x+p) = f(x)
for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f.
Trigonometric functions are commonly used to model periodic phenomena due to their periodicity; no matter what point we start at on the unit circle, if we travel a distance of 2π (360°) along the unit circle from that point, we will arrive back at our starting point. If we look at the sine function, we will find that it repeats every 2π, so 2π is the period of the sine function. We can write this as:
sin(θ+2π) = sin(θ)
To account for multiple full rotations, this can also be written as
sin(θ+2πn) = sin(θ)
where n is an integer.
The figure below shows an example of this periodicity.
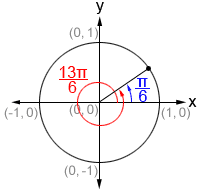
In blue, we see that .
. If we add 2π to
, we get the angle shown in red,
. As can be seen in the figure, even though there is a different degree of rotation in both angles, their terminal sides are exactly the same, meaning that
. We could add another 2π, and would still see that
has the same sine value as
. This is the nature of periodic functions.
are referred to as coterminal angles; they are angles with the same initial and terminal sides, but with different rotations.
Examples:
1.
2.
Graph of the sine function
The graph of sine is periodic, meaning that it repeats itself indefinitely and has a domain of -∞<x<∞. The sine graph has an amplitude of 1; its range is -1≤y≤1. Below is a graph of y=sin(x) in the interval [0,2π], showing just one period of the sine function.
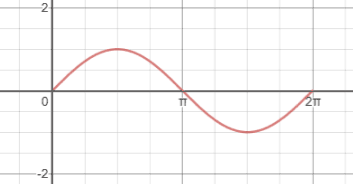
Repeating this portion of y=sin(x) indefinitely to the left and right side would result in the full graph of sine. Below is a graph showing four periods of the sine function in the interval [-4π,4π].
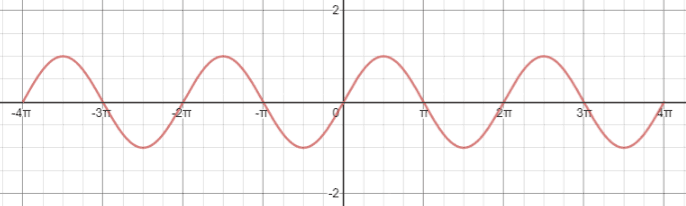
In this graph, we can see that y=sin(x) exhibits symmetry about the origin; if the graph is reflected about the origin, it creates a mirror image. This confirms that sine is an odd function, since -sin(x)=sin(-x).
General sine equation
The general form of the sine function is
y = A·sin(B(x – C)) + D
where A, B, C, and D are constants. To be able to graph a sine equation in general form, we need to first understand how each of the constants affects the original graph of y=sin(x), as shown above. To apply anything written below, the equation must be in the form specified above; be careful with signs.
A—the amplitude of the function; the height from the center of the graph to a maximum or minimum. In y=sin(x), the center is the x-axis, and the amplitude is 1, or A=1, so the highest and lowest points the graph reaches are 1 and -1, the range of sin(x).
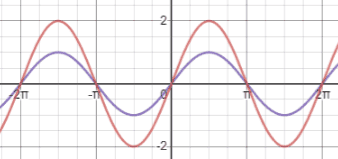
Compared to y=sin(x), shown in purple below, the function y=2 sin(x) (red) has an amplitude that is twice that of the original sine graph.
B—used to determine the period of the function; the period of a function is the distance from peak to peak (or any point on the graph to the next matching point) and can be found as . In y=sin(x) the period is 2π. We can confirm this by looking at the sine graph. Referencing the figure above, we can see that the shape of the sine graph between [-2π, 0] is equivalent to that from [0, 2π] meaning that it repeats itself over an interval of 2π; ie, it has a period of 2π.
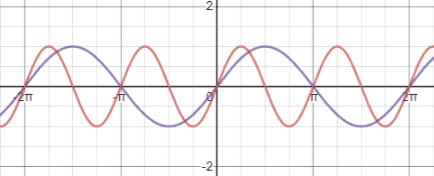
Compared to y=sin(x), shown in purple below, which has a period of 2π, y=sin(2x) (red) has a period of
. This means that the graph repeats itself every π rather than every 2π.
C—the phase shift of the function; phase shift determines how the function is shifted horizontally. If C is negative, the function shifts to the left. If C is positive the function shifts to the right. Be wary of the sign; if we have the equation
then C is
not
, because this equation in standard form is
. Thus, we would shift the graph
units to the left.
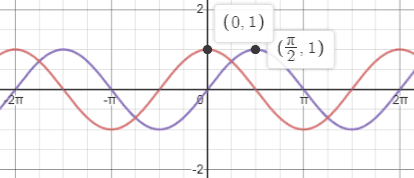
The figure below shows y=sin(x) (purple) and (red). Using one of the peaks of the sine graph as a reference, we can see that the peak at
has been shifted
to the left from its original position and is now at (0,1).
D—the vertical shift of the function; if D is positive, the graph shifts up D units, and if it is negative, the graph shifts down.
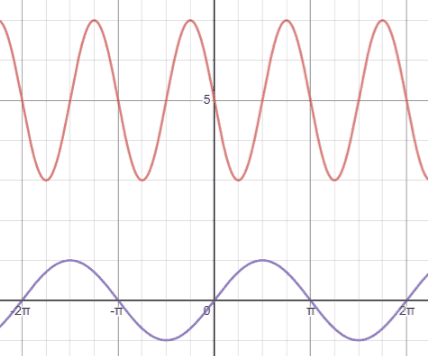
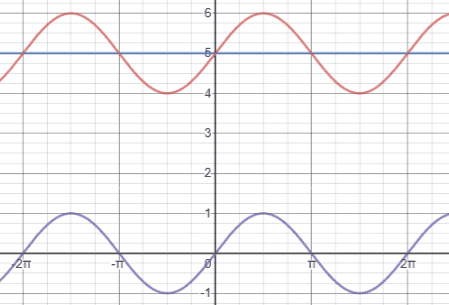
Compared to y=sin(x), shown in purple below, which is centered at the x-axis (y=0), y=sin(x)+5 (red) is centered at the line y=5 (blue).
Putting together all the examples above, the figure below shows the graph of (red) compared to that of y=sin(x) (purple).