Discontinuity

Functions are classified as continuous or discontinuous. Informally, a discontinuous function is one whose graph has breaks or holes; a function that is discontinuous over an interval cannot be drawn/traced over that interval without the need to raise the pencil. The figure below shows two functions with different types of discontinuities:

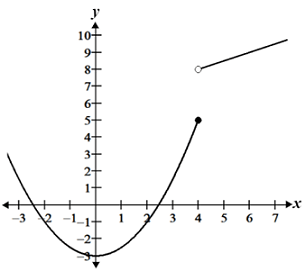
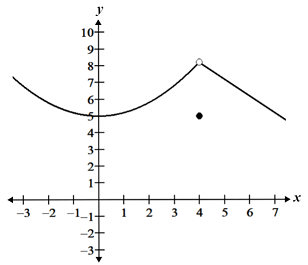
The function on the left exhibits a jump discontinuity and the function on the right exhibits a removable discontinuity, both at x = 4. These types of discontinuities are discussed below.

The formal definition of discontinuity is based on that for continuity, and requires the use of limits. A function f(x) has a discontinuity at a point x = a if any of the following is true:

1. f(a) is undefined.


2. does not exist.


3. f(a) is defined and the limit exists, but .

Each of these cases tests discontinuity at a single point, and the function below provides an example of each of these cases.

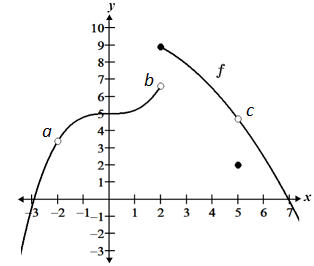
The function is discontinuous at point a because it is undefined; it is discontinuous at point b because the limit of f(x) does not exist at that point since the left and right-handed limits are not equal; it is discontinuous at point c because while the limit exists, f(5) and the limit as x approaches 5 have different values.

Note that continuity is typically tested at a single point, or over a given interval. For a function to be continuous over a given interval, it must be continuous at every point over that interval. Referencing the function above, we could say that it is continuous over various intervals, such as [-1, 1], but that it is discontinuous over the interval [-3, 7] since there are 3 discontinuities within that interval. Thus, when determining the continuity of a function, the interval of interest is an important factor.

Types of discontinuities

Discontinuities are typically categorized as removable or non-removable (jump/infinite).

Removable discontinuity

A removable discontinuity is a discontinuity that results when the limit of a function exists but is not equal to the value of the function at the given point. It is referred to as removable because the function can be re-defined as a piecewise function such that it becomes continuous. For example, refer to the graph below:

The function has a discontinuity at x = 3, where the limit of the function is 6. However, we see that the function is defined at x = 3, and has a value of 4. Thus, the graph represents the function except that it has a hole at x = 3, and we can define the function as a piecewise function to remove the discontinuity:

Since f(3) = 4 but , f(x) has a removable discontinuity at x = 3, and can be said to be continuous for all x.

Non-removable discontinuity

A non-removable discontinuity is a discontinuity in which the limit of the function does not exist. For a limit to exist, the left and right-handed limits must be equal. Thus, for a function to have a non-removable discontinuity, the left and right-handed limits cannot be equal. Unlike removable discontinuities, a function with a non-removable discontinuity cannot be re-defined in such a way that the function becomes continuous.

Two types of non-removable discontinuities include jump discontinuities and infinite discontinuities:

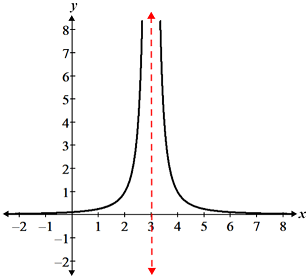
Jump discontinuity	Infinite discontinuity

In both cases, the limit of the function does not exist. For the jump discontinuity, the left and right handed-limits have different values, so the two-sided limit does not exist. Similarly, for the infinite discontinuity, as x approaches 3 from both the left and right side, the function gets closer and closer to +∞. However, the left and right-hand sides of the function can never be equal because of the vertical asymptote, so the limit does not exist. Since the limit does not exist in both cases, the functions have non-removable discontinuities.