Limits and continuity
The concepts of limits and continuity form the foundation of the study of calculus.
Limits
A limit is the value that a function approaches as its input value approaches some value. It provides information about a function's behavior near a point, rather than exactly at that point, which is important since determining the behavior of a function at a specific point is not always possible.
For example, consider the expression . If we evaluate the expression at x = 3, we find that it is undefined, since the x - 3 in the denominator would evaluate to 0. The concept of limits allows us to study the behavior of the function as x gets closer and closer to a given point (in this case 3), even though we cannot evaluate it at exactly that point. In other words, rather than evaluating the expression at x = 3, we find the limit as x approaches 3. This is denoted in limit notation as:
There are a number of different ways to evaluate the limit of a function at a given point, including graphically, numerically, or in some cases, by simply evaluating the limit at the given point. In this case, it is possible to evaluate the limit using the third option, by factoring the numerator, thereby allowing us to cancel the denominator:
The graph of the function is shown in the figure below:
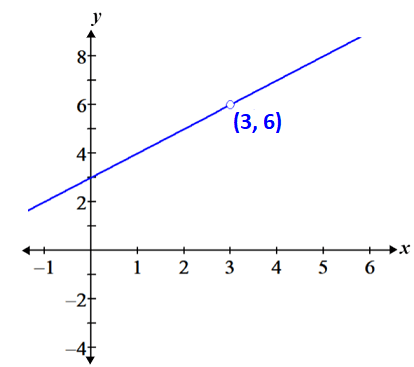
As we determined above, the function is undefined at the point x = 3. Limits allow us to describe the behavior of the function at x = 3 and state that the function approaches 6 even though the function is undefined at that point. It also provides the means for us to discuss another far-reaching concept in calculus, that of continuity. The function above is said to be discontinuous at x = 3, depicted as the open circle in the figure above.
Continuity
Functions can be either continuous or discontinuous. Informally, a function is said to be continuous if its graph is a single unbroken curve with no holes. One way to determine whether or not the graph of the function is continuous is to attempt to draw/trace the function without needing to lift the pencil; if it can be drawn without lifting the pencil, the function is continuous; otherwise, the function is discontinuous. Referencing the figure above, at the point (3, 6), one would have to lift their pencil to draw the graph, so it is discontinuous. On the other hand, the figure below is an example of a continuous function:
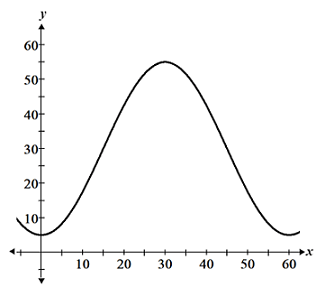
It is possible to trace the entire function without the need to raise the pencil. There are no holes, no jumps, no asymptotes, or any other form of discontinuity.
Continuity is formally defined using limits. A function is continuous at a point x = a if the function exists at that point and if
To extend this definition to the rest of the function, a function is continuous over a given interval if it is continuous at each point in that interval. Again referencing the example of and its graph,

we may say that f(x) is continuous over the interval (-∞, 3) and (3, ∞), but we cannot say that it is continuous over the interval (-∞, ∞) because it is discontinuous at x = 3.
Together, the concepts of limits and continuity provide a basis for the study of calculus, since we need to be able to determine that a function is continuous before moving on to other concepts such as differentiation.
