Horizontal asymptote
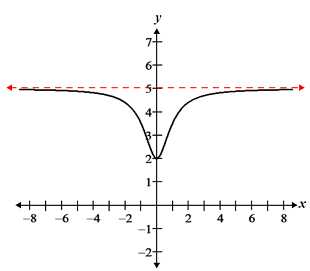
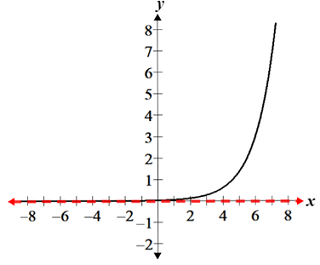
A horizontal asymptote is a horizontal line that the graph of a function approaches as x approaches ±∞. It is not part of the graph of the function. Rather, it helps describe the behavior of a function as x gets very small or large. This is in contrast to vertical asymptotes, which describe the behavior of a function as y approaches ±∞. The dotted red lines in the figure below represent the horizontal asymptotes of the given functions:
|
|
The function on the left has a horizontal asymptote at y = 5, while the function on the right has one at the x-axis (y = 0).
Formally, horizontal asymptotes are defined using limits. A function, f(x), has a horizontal asymptote, y = b, if:
If either (or both) of the above is true, then f(x) has a horizontal asymptote at y = b.
Identifying horizontal asymptotes for rational functions
To find a horizontal asymptote for a rational function of the form , where P(x) and Q(x) are polynomial functions and Q(x) ≠ 0, first determine the degree of P(x) and Q(x). Then:
- If the degree of Q(x) is greater than the degree of P(x), f(x) has a horizontal asymptote at y = 0.
- If the degree of P(x) is equal to that of Q(x), f(x) has a horizontal asymptote that is the ratio of the coefficients of the highest degree term of P(x) to that of Q(x).
- If the degree of P(x) is greater than the degree of Q(x), f(x) has no horizontal asymptote, though it may have a slant asymptote (if the degree of P(x) is 1 greater than that of Q(x).
Examples
Find any horizontal asymptotes for the following functions:
1.
2.
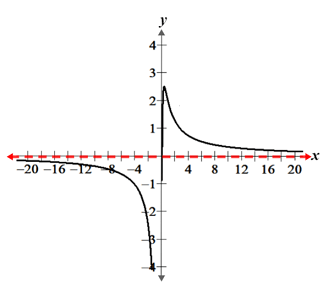
1. The degree of P(x) is 2 and the degree of Q(x) is 3. This corresponds to the first case described above, where the degree of Q(x) is greater than that of P(x). Thus, f(x) has a horizontal asymptote at y = 0, as confirmed by its graph:
2. The degree of P(x) is 4 and the degree of Q(x) is 4. This corresponds to the second case described above, where the degrees of P(x) and Q(x) are equal. Thus, f(x) has a horizontal asymptote at the ratio of the coefficients of the highest degree term of P(x) to Q(x), or 4:2. Thus, f(x) has a horizontal asymptote at y = 4/2 = 2, as shown in the graph of the function:
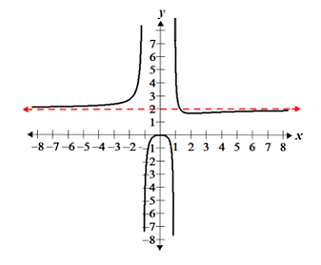
Notice that f(x) crosses its horizontal asymptote on the right of the y-axis. It is possible for a function to cross a horizontal asymptote. In fact, it is possible for a function to cross its horizontal asymptote numerous times, as in the case of an oscillating function.
Finding horizontal asymptotes using limits
The method described in the previous section works for rational functions comprised of polynomials. For rational functions that aren't comprised of polynomials, we can find horizontal asymptotes by computing the limit of the function as x approaches ±∞. A function f(x) will have a horizontal asymptote at y = b, where b is a constant, if either
Example
Find any horizontal asymptotes for the function:
To determine the limit of the function as x approaches ±∞, we must first manipulate the function algebraically such that the limit will not result in an indeterminate form. For the first case, we will consider the limit as x approaches -∞, and divide the function by x2; doing so prevents us from acquiring a result of the form -∞/∞ when computing the limit.
Based on this result, we cannot say that the function has any horizontal asymptote, and we must find its limit as x approaches +∞. In this case, we instead divide by ex to avoid acquiring a result of the form ∞/∞.
Since this is a constant, we conclude that f(x) has a horizontal asymptote at y = 3.
Horizontal vs. vertical asymptotes
While both horizontal and vertical asymptotes help describe the behavior of a function at its extremities, it is worth noting that they do have some differences. One of the key differences is that a function can only have a maximum 2 horizontal asymptotes; it can have 0, 1, or 2 horizontal asymptotes, but no more. We can see why by considering how we find horizontal asymptotes by examining the limit of a function as it approaches ±∞. Since there are only two directions we can consider, -∞ or +∞, there can only be, at maximum, 2 horizontal asymptotes. In contrast, it is possible for a function to have any number of vertical asymptotes. The tangent function for example, has an infinite number of vertical asymptotes. An example of a function that has 2 horizontal asymptotes is f(x) = arctan(x), the graph of which is shown below.
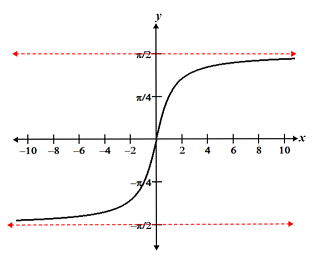
Another important difference between horizontal and vertical asymptotes is that while the graph of a function never touches a vertical asymptote, it is possible for the graph of a function to touch, and even cross a horizontal asymptote; it can do so an infinite number of times, such as in the case of an oscillating function:
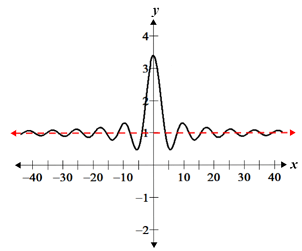
As x approaches ±∞, the function approaches the horizontal asymptote y = 1, but at any given point may be above or below 1 due to its oscillating nature. A function can cross a horizontal asymptote because it still approaches the same value while oscillating about that value. In the case of a vertical asymptote, it is not possible for the function to ever touch or cross the asymptote because vertical asymptotes arise where a function is undefined. The function may approach ±∞, but it is never possible for the function to reach ±∞, which is what crossing a vertical asymptote would imply.
