Interval
An interval is the range of real numbers between two given real numbers. For example, "the set of numbers greater than or equal to four and less than or equal to seven" is an interval that includes all numbers between 4 and 7, including 4 and 7.
Intervals are particularly useful for describing the domain and range of a function, so it is important to be familiar with the various notations used to describe an interval.
Inequalities and interval notation
Inequalities are one way to denote an interval. The interval described above can be expressed using inequalities as 4 ≤ x ≤ 7. The "≤" symbol, like the "≥" symbol, indicates that the end values (4 and 7) are included within the interval. If, instead, the interval were 4 < x < 7, this would mean that 4 and 7 are not included within the interval. Notice that expressing intervals using inequalities is much more concise than doing so with words, allowing us to efficiently discuss intervals in various mathematical contexts.
Another commonly used and closely related method for denoting intervals is aptly named interval notation. Specifying an interval using interval notation is quite similar to doing so using inequalities, except that it instead makes use of parentheses and brackets to denote whether or not the end values of the interval are included:
- [] - brackets indicate a closed interval. This means that the end values are included within the interval. Using our first example, we would express the interval as [4, 7].
- () - parentheses indicate an open interval. This means that the end values are not included. The interval (4, 7) is made up of all values between 4 and 7, not including 4 and 7.
- [) or (] - a combination of brackets and parentheses can be used to indicate a half-bounded interval. The interval [4, 7) includes all real numbers between 4 and 7, as well as 4.
The table below provides a comparison between expressing intervals in interval notation and using inequalities, where a and b are real numbers. It also provides a visual representation of an interval using number lines.
| Interval notation | Inequalities | Number line |
|---|---|---|
| [a, b] | a ≤ x ≤ b |

|
| (a, b) | a < x < b |

|
| (a, b] | a < x ≤ b |

|
| [a, b) | a ≤ x < b |

|
Additionally, intervals can be described as bounded, left-bounded, right-bounded, or unbounded. A left-bounded interval is one in which some real value is smaller than all of its elements, such as 4 < x. A right-bounded interval is one in which some value is larger than all its elements, such as x < 4. A bounded interval is one that is both left and right-bounded, while an unbounded interval is one that does not meet the conditions of a bounded interval. Intervals that are only bounded at one end value are referred to as half-bounded. It is also worth noting that intervals involving infinity should always be denoted as an open interval, since it is not possible to ever equal ± infinity.
Examples
Convert the following inequalities to interval notation.
1. -20 ≤ 3x + 1 < 16:
To convert the inequality to interval notation, we first need to simplify it.
Referencing the above, we can then convert this inequality to interval notation: [-7, 5).
2. 5x + 7 ≥ 30
Thus, the inequality in interval notation is: [25/5, ∞).
Union of inequalities
Union (∪) is a basic set operation used to combine sets. In some cases, we need to combine intervals (such as describing the domain of a function that is only defined over certain intervals), and since intervals are comprised of sets of real numbers, we can use this operation to combine them.
The union of two sets creates a new set that contains all the elements of both sets. For example, given sets A = {1, 2, 3} and B = {4, 5, 6}, A ∪ B = {1, 2, 3, 4, 5, 6}. Note that the union operation can also be read as "or," since the result of a union of sets A and B is comprised of all elements that are either in A "or" B. We can combine inequalities in a similar way. Given the interval described by x < -3 or 1 ≤ x < 5, we can combine the two as follows:
(-∞, -3) ∪ [1, 5)
Example
Using interval notation, specify the interval depicted on the number line.
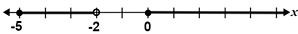
[-5, -2) ∪ [0, ∞)
