Limit

A limit is the value that a function approaches as its input value approaches some value. Limits are denoted as follows:

The above is read as "the limit of f(x) as x approaches a is equal to L."

Limits are useful because they provide information about a function's behavior near a point. Consider the function f(x) = x + 3. The figure below is a graphical representation of the limit of f(x) as x approaches 3.

The blue arrows indicate the directions from which we approach x = 3, and the y value that f(x) approaches at x = 3 is its limit at that point. In this case, we see that the function approaches a y value of 6 (denoted by the red circle) as we get closer and closer to 3 from both the left and right sides. Thus, the limit of f(x) = x + 3 as x approaches 3 is 6, or using limit notation:

Notice that the limit in this example is equal to the value of the function at x = 3. In other words:

The difference between the limit of a function and the value of that function at a given point is that a limit is not dependent on the value of the function existing. Thus, it may be possible to determine the limit of a function at a point even if it is undefined at that point. The graph below of is almost identical to f(x) = x + 3, except that it is undefined at x = 3, as depicted by the open circle:

Even though the function is undefined at x = 3, the limit as x approaches 3 is still 6. This is important because in certain cases (such as with derivatives), we want to determine the behavior of a function at a point, regardless of whether or not the function exists at that point. Also, it is worth noting that even in cases where the function exists at the given point, the value of the function is not necessarily the same as the limit at that point.

The above example is a graphical representation of a limit. It is also possible to conceptualize limits numerically. Consider the same function used above: . Although the function is undefined at x = 3, we know that limits are not affected by the value of the function at the point of interest, so we can evaluate the function at surrounding x values that are close to but not equal to 3 in order to determine the limit:

This confirms what we determined graphically, that as x gets closer and closer to 3 from the left or right side, the function value approaches a value of 6. While the numerical approach to determining a limit is helpful for illustrating the concept of a limit, it worth noting that it is often not as efficient or effective as other methods.

One-sided limits

There are a few different types of limits. Typically, a two-sided limit is simply referred to as a "limit." The examples above are examples of two-sided limits (referred to as limits for the rest of the article). One of the conditions for a limit to exist is that the value the function approaches from both the left and right sides must be the same. When the values approached from the left and right sides are not equal, the limit does not exist (DNE). In some cases, simply knowing that the limit does not exist does not provide sufficient information about the behavior of the function at or around the point of interest. In these cases, examining the one-sided limits can provide more information about the function. Consider the graph of the function shown below:

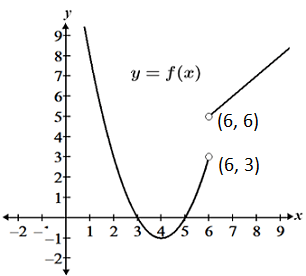
The limit of f(x) does not exist at x = 6 because its left and right-handed limits are not equal, but evaluating the left and right-handed limits allows us to determine that the function has a jump discontinuity at x = 6.

One-sided limits differ from two-sided limits only in terms of the domain of the function that is considered when determining the value of the limit. Given that a function is defined over the relevant intervals, a left-handed limit is one in which the value of the function approaches some limit, L, as x approaches some value, a, in the interval. A right-handed limit is similarly defined, except that the interval of interest is the domain of the function to the right of a.

One-sided limits are denoted in much the same way as two-sided limits, with the exception that a + and - symbol are used to indicate right and left-handed limits, respectively:

• Left-handed limit:


• Right-handed limit:

It is worth noting that it is also possible for one-sided limits to not exist. This occurs at vertical asymptotes, or when a function oscillates to such a degree that it is not possible to narrow the limit down to any particular value.

Finding limits

There are a number of different methods used to find the limit of a function, including substitution, factoring, rationalization, the squeeze theorem, and more.

Substitution

Substitution is a method that involves evaluating the function at the point of interest. Generally, it can only be used for simpler functions in which the function is defined at x = a and the limit is equal to the value of the function at a. For example, given that we want to find the limit of f(x) = x² - 9 as x approaches 4, we would simply plug 4 into the function and evaluate it:

While it would be ideal if all limits could be computed using substitution, there are many cases, particularly when working with rational functions, where substitution cannot be used. These occur when the function doesn't exist at the point of interest, or if some indeterminate form results from substitution. Indeterminate forms include the following:

An indeterminate form simply means that after attempting substitution, the expression is in a form that does not provide enough information for us to determine the limit. It is possible that the limit may not exist, or that we can determine the limit using other methods. Note that while many indeterminate forms involve infinity, a limit whose value is negative infinity or infinity is not indeterminate. Rather, it is a different type of limit referred to as an infinite limit.

Factoring

Factoring is one of the methods that can be used to evaluate the limit of a function that has an indeterminate form. Specifically, it can be used for functions in which factored terms in the numerator and denominator cancel out, causing the function to no longer be an indeterminate form.

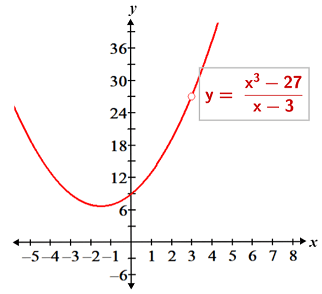
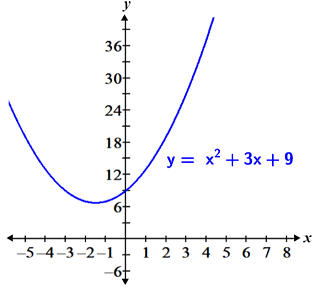
Rationalization

Rationalization is another method that can be used to find the limit of an indeterminate form. Rationalization refers to multiplying an expression by its conjugate in an effort to simplify the function. The goal of rationalization is the same as that of factoring, with the difference between the two being the types of expressions the methods can be used to simplify.

Squeeze theorem

The squeeze theorem, also referred to as the sandwich theorem, or pinching theorem, is another method used to find a limit. It can be used in certain cases when methods such as factoring and rationalization wouldn't work. The squeeze theorem is defined as follows:

Let f(x), g(x), and h(x) be functions such that for all x values over some interval containing a, except maybe at a,

In addition, suppose that

.

Then:

In other words, since f(x) is squeezed between g(x) and h(x), if g(x) and h(x) have the same limit at a, f(x) must also have the same limit.

To use the squeeze theorem, we need to find functions that are similar enough to f(x) that we can be sure that it is squeezed between g(x) and h(x). We also want to choose functions such that the limits of g(x) and h(x) are easier to calculate.

Note that there are other ways to evaluate limits, but these are some of the most common that don't involve the use of derivatives. Refer to the L'Hopital's rule page for a method of computing difficult limits that involves derivatives.