Domain and range
The domain and range of a function is all the possible values of the independent variable, x, for which y is defined. The range of a function is all the possible values of the dependent variable y. In other words, the domain is the set of values that we can plug into a function that will result in a real y-value; the range is the set of values that the function takes on as a result of plugging in an x value within the domain of the function.
In mathematical terms, given a function f(x), the values that f(x) can take on constitute the range of the function, while all the possible x values constitute the domain. Consider the function f(x) = x2.
Example:
f(x) = x2
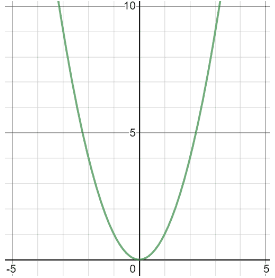
There are no x-values that will result in the function being undefined and matter what real x-value we plug in, the result will always be a real y-value. Thus, the domain of f(x) = x2 is all x-values. Then, from looking at the graph or testing a few x-values, we can see that any x-value we plug in will result in a positive y-value. Thus, the range of f(x) = x2 is all positive y-values.
Notice in the examples above that we described the domain and range using words. While this is possible for all functions, different notations have been developed for expressing domains and ranges in a more concise way. This makes it far easier to express the domains and ranges of multiple functions at a time, particularly as functions get more complicated. Two of these notations are interval notation and set notation.
Interval notation
When using interval notation, domain and range are written as intervals of values. The table below shows the basic symbols used in interval notation and what they mean:
| Name | Symbol | Meaning |
|---|---|---|
| Parentheses | ( ) | Endpoints not included (exclusive) |
| Brackets | [ ] | Endpoints included (inclusive) |
| Union | ∪ | "or" - used to combine two or more sets |
When indicating the domain in interval notation, we need to keep the following in mind:
- The smallest term in the interval is written first, followed by a comma, and then the largest term.
- The first term is the left endpoint and the second term is the right endpoint.
- The endpoints are written between either parentheses or brackets, depending on whether the endpoint is included or not.
Let's look at the same example as above, f(x) = x2 to see how interval notation is used. Recall that the domain of f(x) = x2 is all real numbers. In other words, any value from negative infinity to positive infinity will yield a real result. Thus, we can write the domain as:
(-∞, ∞)
We used parentheses rather than brackets around each endpoint because the endpoints are negative and positive infinity, which by definition have no bound. Recall that the range of f(x) = x2 is all positive y-values, including 0. The range can therefore be written in interval notation as:
[0, ∞)
The union symbol is used when we have a function whose domain or range cannot be described with just a single interval. The union symbol can be read as "or" and it is used throughout various fields of mathematics. In the context of interval notation, it simply means to combine two given intervals. For example, consider the function:
This is the same as our function above, except that it is not defined over the interval (0, 1). The domain of the function is therefore all x-values except those in the interval (0, 1), which we can indicate in interval notation using the union symbol as follows:
(-∞, 0] ∪ [1, ∞)
Note that it is also possible to use multiple union symbols to combine more intervals in the same manner.
Set notation
When using set notation, also referred to as set builder notation, we use inequality symbols to describe the domain and range as a set of values. Like interval notation, there are a number of symbols used in set notation, the most common of which are shown in the table below:
| Name | Symbol | Meaning |
|---|---|---|
| Braces | { } | "the set of" - indicates a set |
| Vertical bar | | | "such that" - symbol is followed by a constraint |
| "Element of" | ∈ | Indicates that an element is a member of some set |
| Double-struck R | ℝ | The set of all real numbers |
| Union | ∪ | "or" - used to combine two or more sets |
Standard inequality symbols such as <, ≤, =, ≠, >, ≥, and so on are also used in set notation.
Using the same example as above, the domain of f(x) = x2 in set notation is:
{x | x∈ℝ}
The above can be read as "the set of all x such that x is an element of the set of all real numbers." In other words, the domain is all real numbers. We could also write the domain as {x | -∞ < x < ∞}.
The range of f(x) = x2 in set notation is:
{y | y ≥ 0}
which can be read as "the set of all y such that y is greater than or equal to zero."
Like interval notation, we can also use unions in set builder notation. However, in set notation, rather than using the symbol "∪," we use the word "or" by convention. For example example, given the function
we can write the domain of the above function in set notation as:
{x | x ≤ 0 or x ≥ 1}
