Even and odd functions

Even and odd are terms used to describe the symmetry of a function. An even function is symmetric about the y-axis of the coordinate plane while an odd function is symmetric about the origin. Most functions are neither even nor odd. The only function that is both even and odd is f(x) = 0.

How to tell if a function is even or odd

We can test the symmetry of a function either algebraically or by inspecting the graph, as detailed below.

Even and odd functions: testing algebraically

For a function to be even, the following must be true:

f(x) = f(-x)

This means that each x value and -x value have the same y value. Thus, to see if a function is even, plug -x into x and simplify. If the resulting function is the same as the original, the function is even.

For a function to be odd, the following must be true:

f(-x) = -f(x)

This means that each x value has a y value that is the opposite of the y value of their corresponding -x value. To see if a function is odd, plug -x into x and simplify. If the resulting function is the original function multiplied by -1, then the function is odd.

If a function does not follow the rule f(x) = f(-x) or f(-x) = -f(x), the function is neither even nor odd. Most functions are neither even nor odd, with the only function being both even and odd being f(x) = 0.

Note that even functions that are polynomials only have even exponents. Odd functions that are polynomials only have odd exponents. This is true only for polynomials however, and there are many other types of functions, such as rational and trigonometric functions, that are even or odd without following this rule.

Even and odd functions: testing graphically

Given a graph of a function, to test whether it is even or odd, consider the symmetry of the graph. Recall that an even function is symmetric about the y-axis while an odd function is symmetric about the origin.

To visualize what this means for an even function, imagine folding the graph along the y-axis. If folding the graph across the y-axis results in the graph folding on top of itself, the function is even. The graph of the parabola centered about the y-axis, shown in the figure below, is an even function:

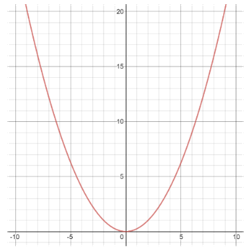
For an odd function, being symmetric about the origin means that if we rotate the graph of the function 180° about the origin, we will wind up with the same graph. Another way to think of this is to first fold the graph along the y-axis, and then the x-axis. Again, if we wind up with the same graph, the function is odd. The following graph is an odd function:

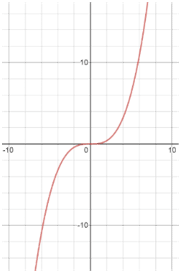
One way to remember the difference between even and odd functions is to remember that both "odd" and "origin" start with the letter "o." Then you just need to remember that the other type of function, even functions, are symmetric about the y-axis.

You will not always have a graph of the function at your disposal, so sometimes you must prove that a function is even or odd (or neither) using algebra.

Properties of even and odd functions

Below are some properties of even and odd functions.

Addition and subtraction properties

The addition and subtraction properties of odd and even functions are as follows:

• even + even = even


• odd + odd = odd


• odd - odd = odd


• even - even = even


• even + odd = neither even nor odd unless one of the functions is f(x) = 0.

Multiplication and division properties

• even × even = even


• odd × odd = even


• even × odd = odd


• even ÷ even = even


• odd ÷ odd = even


• even ÷ odd = odd