Rational function

A rational function is a function made up of a ratio of two polynomials. Rational functions follow the form:

In rational functions, P(x) and Q(x) are both polynomials, and Q(x) cannot equal 0.

The parent function of rational functions is .

Example

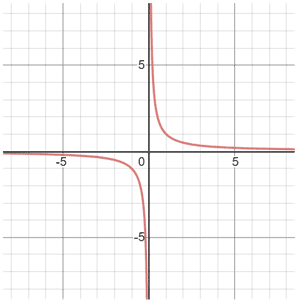
As you can see, is made up of two separate pieces. Most rational functions will be made up of more than one piece.

In addition, notice how the function keeps decreasing as x approaches 0 from the left, and how it keeps increasing as x approaches 0 from the right. This is because if x = 0, then the function would be undefined.

Try to picture an imaginary line x = 0. The function never touches this line but gets very close to it. This is what we call a vertical asymptote. Vertical asymptotes occur at x-values when the denominator of a rational function equals 0 and the numerator does not equal 0.

Try to picture an imaginary line y = 0. Again, the function never touches this line, but gets very close to it. This is what we call a horizontal asymptote. The value of horizontal asymptotes depends on certain characteristics of the polynomials in the rational function.

Example

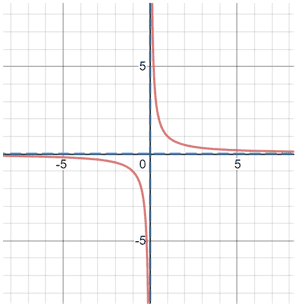
You will learn more about asymptotes later on. This is simply a brief introduction to the topic.

To transform the rational function , you can apply the general expression for function transformations.

See also function transformations.