Parabola
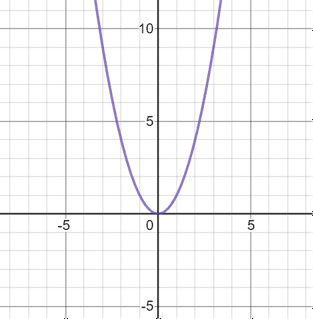
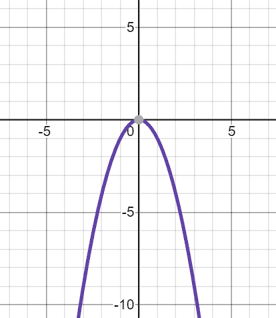
A parabola is the characteristic U-shaped curve of a quadratic equation. A parabola can be used to model many real-world phenomena. For example, when you shoot a basketball, the path of the ball creates a parabola. Below are two parabola graph examples, one in which the parabola opens upwards and one in which it opens downwards:
|
|
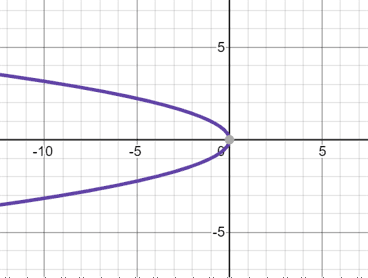
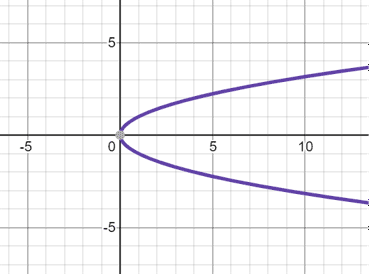
Note that a parabola does not have to be vertical, but horizontal parabolas are not functions (they fail the vertical line test). Some functions you see will be horizontal parabolas with restricted domains (e.g. ). You will learn more about these when you explore conics.
Example
|
|
What is a parabola
The precise parabola definition is: a collection of points such that the distance from each point on the curve to a fixed point (the focus) and a fixed straight line (the directrix) is equal.
Parts of a parabola
The figure below shows the various parts of a parabola as well as some important terms.

- Focus - the fixed point of a parabola.
- Directrix - the line perpendicular to the parabola's axis of symmetry.
- Vertex - the midpoint between the focus and directrix along the axis of symmetry of the parabola; this is the point at which the parabola changes direction as well as where the graph is most curved. It is also the minimum or maximum of a quadratic function.
- Axis of symmetry - the line that splits the parabola through the middle; it passes through the vertex, focus, and directrix.
- Latus rectum - a chord that passes through the focus that is parallel to the directrix and perpendicular to the axis of symmetry.
- Eccentricity - the ratio of the distance of a point from its focus to its distance from the directrix (always 1 for a parabola).
- Focal length - the distance between the focus and the vertex measured along the axis of symmetry.
Focus and directrix
The focus and directrix are the two parts that define a parabola. In the figure shown above, point q is equidistant from both the focus and the directrix. A parabola is formed by the set of all points that are equidistant from the focus and directrix.
Note that the focus is always inside of the parabola and on the axis of symmetry. A parabola opens in the direction of the focus. Also, the direction in which a parabola opens never changes.
The directrix is always on the outside of the parabola, on the opposite side from which the parabola opens and perpendicular to the axis of symmetry. The parabola never intersects the directrix.
Properties of parabolas
Below are some basic properties of parabolas:
- A parabola has an eccentricity of 1.
- A parabola is symmetric about its axis.
- A parabola's axis of symmetry is perpendicular to the directrix.
- A parabola's axis of symmetry passes through its focus and vertex.
- The tangent at the vertex of a parabola is parallel to its directrix.
- A parabola's vertex is the midpoint of the focus and directrix through its axis of symmetry.
Parabola equation
The equation of a parabola is typically written in standard form or vertex form, as described below.
Standard form of a parabola
The standard form of a parabola (also referred to as the conic equation of a parabola) is,
(vertical axis)
or
(horizontal axis)
where (h, k) is the vertex of the parabola and p is its focal length.
How to find focus and directrix using standard form
For the vertical parabola equation,
- If p > 0,
- the parabola opens upwards
- the focus is at: (h, k + p)
- the equation of the directrix is: y = k - p
- If p < 0,
- the parabola opens downwards
- the focus is at: (h, k - p)
- the equation of the directrix is: y = k + p
- The vertex is at (h, k).
- The equation for the axis of symmetry is x = h.
For the horizontal parabola equation,
- If p > 0,
- the parabola opens to the right
- the focus is at: (h + p, k)
- the equation of the directrix is: x = h - p
- If p < 0,
- the parabola opens to the left
- the focus is at: (h - p, k)
- the equation of the directrix is: x = h + p
- The vertex is at (h, k).
- The equation for the axis of symmetry is y = k.
If the vertex of the parabola is at the origin (0, 0), the above equations simplify to:
(vertical axis)
or
(horizontal axis)
We will not show the derivation of the general equation of a parabola here, but it is found by setting the expressions for the distance between the focus and some point on the parabola (shown in pink in the parts of a parabola figure above) equal to the expression for the distance between the directrix of the parabola to that same point. Since we know that those distances are equal, setting the expressions equal to each other then solving for y yields the standard form of a parabola. Also, it is worth noting that p represents the focal length, which is the distance along the axis of symmetry from the vertex to the focus (or directrix).
How to convert standard to vertex form
To convert the standard (conic) form of a parabola to vertex form, we need to first rearrange the standard form by solving for y. The conic equation of a parabola is:
Solving for y yields:
The term in the above equation is equivalent to the "a" in the vertex form of a parabola, making the re-arranged form equivalent to vertex form. We will not go over why this is the case, but it has to do with the derivation of the conic equation of a parabola. It is worth noting that the conic equation of a parabola more readily provides information about the parabola because p is the focal length, which can be used to determine many other characteristics of the parabola.
Example
Convert to vertex form.
In the above equation, the vertex of the parabola is at (2, 5) and 4p = 1, so p = ¼. Solving the equation for y yields,
which is the vertex form of a parabola. We can confirm by testing the value of p in this form, knowing that . Since a = 1, we can solve for p as:
This is the same result obtained above so the equations are equivalent.
Converting the horizontal form of the standard form of a parabola is similar, except that we solve for x instead of y.
Vertex form of a parabola
The vertex form of a parabola is the form of a parabola derived from completing the square of the general form of a quadratic equation. The equations are as follows,
(vertical axis)
or
(horizontal axis)
where the vertex is (h, k) and a is the distance from the vertex to the focus. Recall that the general form of a quadratic equation is,
where a, b, and c are constants, and a ≠ 0. Completing the square yields:
Setting and
yields the vertex form of a parabola,
. The same process is used for the horizontal equation.
How to find focus and directrix using vertex form
Referencing the above section, we can see that it is relatively simple to find values for important parts of the parabola such as the focus, directrix, axis of symmetry, and vertex. While it is also simple to find the vertex from the vertex form of a parabola, finding the other values is slightly more complicated. To do so, we use the equation for the vertex form prior to substituting h and k to find that,
- If a > 0
- The parabola opens upwards
- The focus is at:
- The equation of the directrix is:
- If a < 0
- The parabola opens downwards
- The focus is at:
- The equation of the directrix is:
- The vertex is at:
- The equation for the axis of symmetry is:
For the horizontal equation,
- If a > 0
- The parabola opens to the right
- The focus is at:
- The equation of the directrix is:
- If a < 0
- The parabola opens to the left
- The focus is at:
- The equation of the directrix is:
- The vertex is at:
- The equation for the axis of symmetry is:
Also, there are some other things worth noting about the constants a, b, and c:
- a - The larger the magnitude of a, the narrower the parabola will be; the closer the magnitude is to 0, the wider the parabola.
- b - b affects the position of the parabola.
- c - c is the y-intercept of the parabola.
Notice that in this form, it is much more tedious to find various characteristics of the parabola than it is given the standard form of a parabola in the section above. The only value that is relatively easy to determine is the vertex when using vertex form. The general form of a quadratic equation, y = ax2 + bx + c is even less useful in this respect. The example below shows a slightly simplified form (though it is essentially the same as above) for finding the directrix and focus of a parabola using vertex form. It uses the fact that the focal length of a parabola, p, is equal to .
The focus of a parabola in vertex form y = a(x- h)2 + k is located at (h, k + ) and the directrix is located at y = k -
.
Example
Find the focus and directrix of .
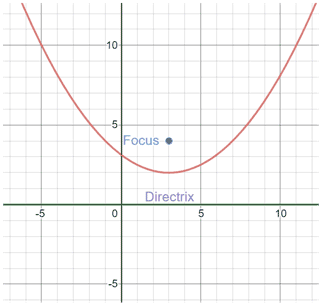
Vertex form of a parabola is also useful because it makes it easy to graph the parabola.
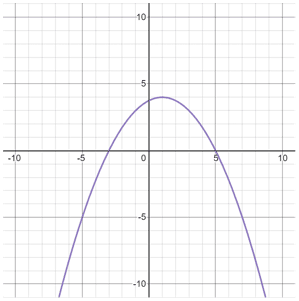
Example
Graph f(x) = -(x - 1)2 + 4.
From this equation, we can determine that the vertex of the parabola is at (1, 4), and the axis of symmetry is at x = 1. Once we know the vertex, we can plug in a few x-values on either side of the vertex to find their corresponding y-values and then graph the parabola.
How to convert vertex form to standard form
To convert the vertex form of a parabola to its standard (conic) form, we use the relationship . The two forms are equivalent except for this difference. Recall the vertex form of a parabola is:
Substituting for a yields:
which is almost the standard form of a parabola. All we need to do is rearrange the equation as follows:
General form of a quadratic equation
The general form of a quadratic equation is:
where a, b, and c are constants and a ≠ 0. If a were equal to 0, the function would be a line not a parabola. Note that parabolas with horizontal axes of symmetry are still parabolas, but they are not functions because they do not pass the vertical line test. The general form of a quadratic equation is typically converted to vertex form for ease of graphing by hand.
How to convert a quadratic equation to vertex form
To convert the general form of a quadratic equation to vertex form, complete the square. You can also convert to vertex form by using the knowledge that the vertex lies on the axis of symmetry.
The x-value of the vertex is x = - , so the y-value is y = f (-
). Plug these values in for h and k in the vertex form equation. Then, a is the same in both forms, so simply copy that to the vertex form equation.
Example
Convert f(x) = x2 - x - 20 to vertex form.
a = 1; b = -1; c = -20
x = h = - = -
=
How to convert from vertex form to a quadratic equation
To convert from vertex form back to the general form of a quadratic equation, f(x) = ax2 + bx + c, expand the equation and then simplify.
Example
Convert f(x) = 5(x + 3)2 - 6 to the general form of a quadratic equation.
f(x) = 5(x + 3)2 - 6
f(x) = 5(x2 + 6x + 9) - 6
f(x) = 5x2 + 30x + 45 - 6
f(x) = 5x2 + 30x + 39
How to find the vertex of a parabola
Finding the vertex of a parabola is dependent upon the form of the equation.
General form of a quadratic equation
The vertex of a parabola given the general form of a quadratic equation f(x) = ax2 + bx + c is located at:
or
Note that:
- If ab < 0, the vertex lies to the right of the y-axis.
- If ab > 0, the vertex lies to the left of the y-axis.
- If ab = 0, the vertex lies on the y-axis.
Vertex form of a parabola
To find the vertex given an equation in vertex form f(x) = a(x - h)2 + k, just find (h, k). The vertex is located at the point (h, k). Just be careful with the signs in the equation.
Standard form of a parabola
To find the vertex given the standard equation of a parabola, (x - h)2 = 4p(y - k), just find (h, k). The vertex is located at the point (h, k). Just be careful with the signs in the equation.
How to find axis of symmetry of a parabola
For quadratic equations in general form ax2 + bx + c, the axis of symmetry can be found using the equation . To find the y-coordinate of the vertex, find the axis of symmetry and substitute that x-value into the original equation.
Example
Find the axis of symmetry of f(x) = x2 + 6x + 11
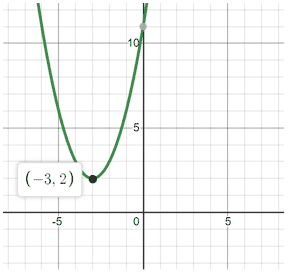
How to find the zeros of a parabola
To find the zeros of a parabola, set f(x) = 0 and solve for x. The zeros of a parabola occur when the function has a y-value of 0, which occurs when the parabola intersects the x-axis. A parabola can have 0, 1, or 2 zeros.
- 0 - A parabola with no zeros either lies above the x-axis and opens upwards (a > 0) or lies below the x-axis and opens downwards (a < 0).
- 1 - A parabola with one zero has its vertex at some point on the x-axis.
- 2 - A parabola with two zeros either has a vertex below the x-axis and opens upwards (a > 0) or a vertex above the x-axis and opens downwards (a < 0).
Example
Find the zeros of f(x) = x2 + 2x - 15
x2 + 2x - 15 = 0
(x + 5)(x - 3) = 0
x = -5; x = 3
Thus, f(x) = x2 + 2x - 15 has two zeros: one at (-5, 0) and the other at (3, 0).
How to sketch a parabola
To sketch a parabola:
- Find the vertex.
- Find the y-intercept.
- Solve f(x) = 0 to find potential x-intercepts.
- Find one point on either side of the vertex (if there are 2 x-intercepts, we can use these)
- Connect the vertex to the points with a curve. The more points we find, the more accurate the shape of the parabola.