Piecewise functions

A piecewise function is made up of two or more functions, each defined on a specific domain. Piecewise functions follow the following format:

The piecewise function above is the absolute value function. As you can see, piecewise functions include:

1. A curly bracket to indicate that the function is comprised of more than one subfunction
2. The subfunctions that make up the piecewise function
3. The subdomains corresponding to each subfunction

The domains of the subfunctions cannot overlap, but one function can end where another starts. If different functions were part of the same domain, the piecewise function would not be a function anymore!

To graph a piecewise function, graph each subfunction at the indicated domain. Be wary of the inequality symbols (< , ≤ , > , ≥) and whether they include or exclude the end of the subdomain. If they include the domain, draw a point and fill it in. If they exclude the domain, draw a point but do not fill it in.

Example

First, graph y = 2x + 3 at x < -3 (open point at x = -3).

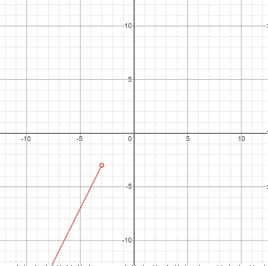
Then, graph y = x² + 3 at -3 ≤ x < 2 (closed at x = -3, open at x = 2).

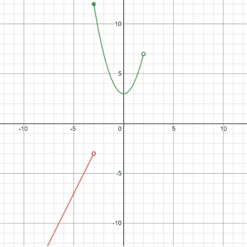
Lastly, graph y = 7 at x ≥ 2 (closed at x = 2).

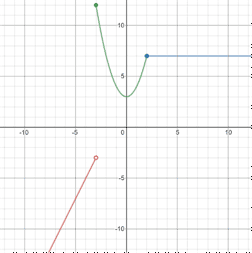
See also inequality symbols, absolute value, inequality.