Hyperbola
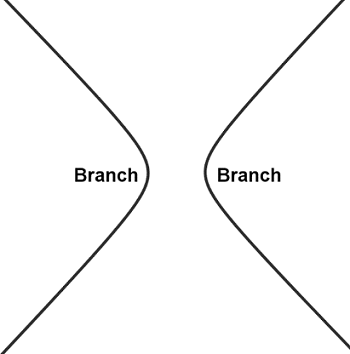
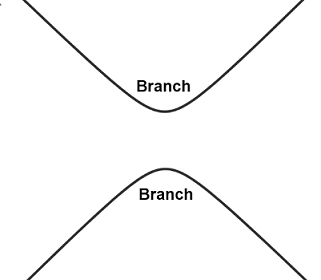
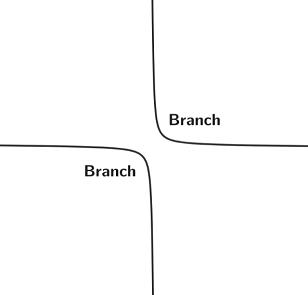
A hyperbola is a two-dimensional curve in a plane. It takes the form of two branches that are mirror images of one another that together form a shape similar to a bow. Below are a few examples of hyperbolas:
|
|
|
Geometrically, a hyperbola is the set of points contained in a 2D coordinate plane that forms an open curve such that the absolute difference between the distances of any point on the hyperbola and two fixed points (referred to as the foci) is constant; refer to the figure below.
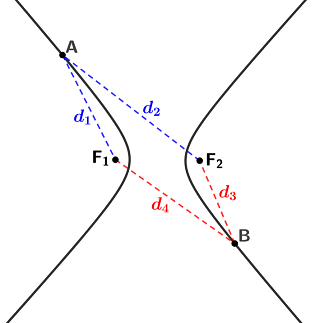
In the figure, 2 points, A and B, are shown. Note that these points are not mirrored versions of each other, so d1 ≠ d3 and d2 ≠ d4. The foci of the hyperbola are points F1 and F2. The absolute difference between point A and the foci is |d1 - d2| and the absolute difference between point B and the foci is |d3 - d4|. For the curve to be a hyperbola, given points A and B, the following must be true:
This will be true of any two points on a hyperbola since the absolute value of the difference remains constant.
Axes and asymptotes of a hyperbola
A hyperbola has an axis of symmetry that passes through its two foci. The points of intersection of the hyperbola and the axis of symmetry are its vertices, and the line segment between the two vertices is referred to as its transverse axis. In the figure below, the vertices are V1 and V2, and F1 and F2 are its foci:
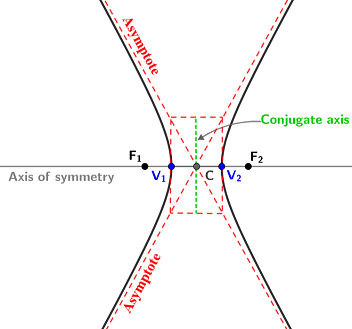
The midpoint of the transverse axis, V1V2, is the center of the hyperbola. The line perpendicular to the transverse axis through its center (C) is referred to as the conjugate axis. The asymptotes of a hyperbola pass through its center as well as through the corners of a rectangle whose width is the transverse axis and whose length is depicted in the section below.
Equation of a hyperbola
The equation of a hyperbola can be written in either rectangular or parametric form.
Standard form of a hyperbola
In the 2D coordinate plane, the standard form for the equation of a hyperbola with center at (h, k), transverse axis of length 2a, and conjugate axis of length 2b can be written in two ways based on whether the hyperbola opens left and right, or up and down:
| Horizontal transverse axis | Vertical transverse axis |
|---|---|
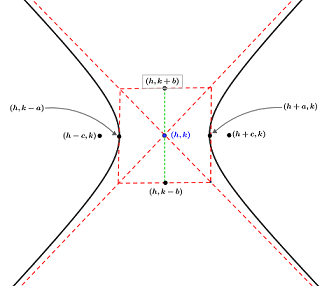
|
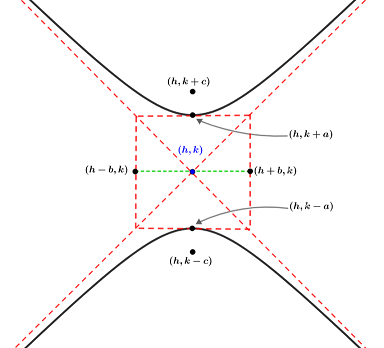
|
| Asymptotes: |
Asymptotes: |
If the center of the hyperbola is the origin, the equation of the hyperbola reduces to either:
(horizontal transverse axis)
or
(vertical transverse axis)
Example
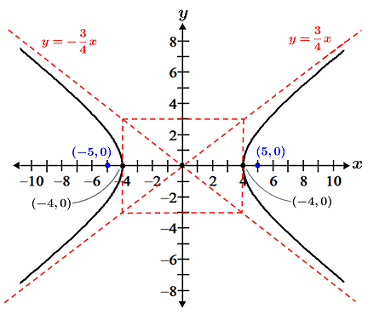
Graph . State the vertices, foci, and asymptotes.
The equation of the hyperbola takes the form of a hyperbola in which the transverse axis is horizontal. The center is at (0, 0), a = = 4, and b =
= 3. Thus, c can be calculated as:
Thus, the vertices are (0 - 4, 0) = (-4, 0) and (0 + 4, 0) = (4, 0). The ends of the conjugate axis are (0, 0 - 3) = (0, -3) and (0, 0 + 3) = (0, 3). The foci are (0 - 5, 0) = (-5, 0) and (0 + 5, 0) = (5, 0). The asymptotes are:
The graph of the hyperbola is shown below:
General form of a hyperbola
The general form of a hyperbola is,
where A, B, C, D, and E are real numbers and A and B have opposite signs. The following example shows how to convert from the general form of a hyperbola to standard form.
Example
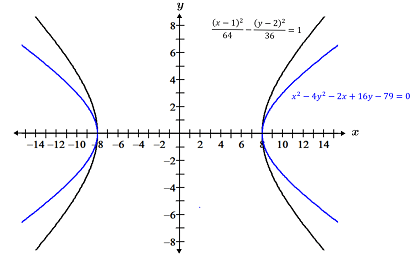
Convert the general form of the following hyperbola, , to standard form.
To find the standard form of the above hyperbola, complete the square with respect to both x and y:
Since the equation for the hyperbola in standard form takes the form , the hyperbola has a horizontal transverse axis.
Parametric form of a hyperbola
Like the standard form for the equation of a hyperbola, there are two forms for the parametric form of a hyperbola based on whether it has a horizontal or transverse axis. Given a hyperbola with center at (h, k), transverse axis with length 2a, and conjugate axis of length 2b, where θ is the angle in standard position, the equations for a hyperbola in parametric form are as follows:
- Horizontal transverse axis -
- Vertical transverse axis -
Example
Write the equation for a hyperbola, , in parametric form.
Since the above equation is that for a hyperbola with a horizontal transverse axis, use the equation . The center of the hyperbola is at (-3, 2), a = 4, and b =
. Thus, the equation for the hyperbola in parametric form is:
We can verify the solution by eliminating the parameter using the trigonometric identity:
Solving the parametric set of equations for sec(θ) and tan(&theta);,
Substituting these values into the identity yields,
which verifies the solution found above.
Eccentricity
The eccentricity (e) of a hyperbola is a measure of the shape of a hyperbola. It is the ratio of the distance between the center of the hyperbola and its foci (c) to the distance between the center of the hyperbola and its vertices (a):
Since the foci of a hyperbola always lie further from the center than its vertices, c > a, so the eccentricity of a hyperbola is always greater than 1. The greater its eccentricity, the wider the branches of a hyperbola open.
Example
Compare the eccentricities of the hyperbolas (i) and
(ii).
For hyperbola i, a = 8 and b = 6, so:
Thus, .
For ii, first complete the square with respect to both x and y to convert the equation to standard form:
Thus, a = 8 and b = 4, so:
Thus, . Since the eccentricity of i is 1.25 while the eccentricity of ii is 1.12, the branches of i open wider than those of ii. Both hyperbolas are shown in the figure below: