Scale
Scale is a concept that is used throughout mathematics and statistics, as well as other applications. Scales that most people have likely encountered include map scales, weighing scales, scale models, graph scales, and more.
The concept of scale is also used in statistics in the form of scales of measurement. Data in statistics is often classified as being one of four measurement scales: nominal, ordinal, interval, or ratio. The level of scale of the data determines how the data is handled and analyzed. Nominal scale, ordinal scale, interval scale, and ratio scale are listed in ascending order. The ratio scale is the fourth and highest level, and therefore most ideal type of data for research and statistical purposes, while the nominal scale is the first level, and most basic type of data.
Nominal scale
A nominal scale is one that is used for the purpose of identification. It is the first level of measurement scale. Examples of data on a nominal scale, or nominal data, include things that someone may fill out on a form, such as hair color, nationality, gender, and employment status.
Most commonly, nominal data is qualitative. In some cases numbers may be considered nominal data, but only if the numbers don't have a quantitative or numeric value, and are used solely for the purpose of identification. For example, when filling out a form, black hair may be assigned to the number 1, blond hair to the number 2, brown hair to the number 3, and so on for all hair colors. Those numbers identify the hair color, and do not have meaning other than the hair color they represent. Any of the numbers could easily have been assigned to any of the other hair colors (1 for blond, 2 for brown, etc.).
Ordinal scale
Data on an ordinal scale has some rank, usually arranged in an ascending or descending order. It is the second level of measurement scale. Examples of ordinal data include the positions in a race (fastest to slowest), a person ranking some of their favorite foods, and the highest to lowest scores on an exam.
Interval scale
An interval scale is the third level of measurement scale. It is an extension of the ordinal scale in that in addition to having ordered numbers, the ordered numbers have the characteristic of being equally spaced apart.
Given an interval scale, not only do you know that a given value on the scale is larger or smaller than another, you can also determine exactly how much larger or smaller the object or measure is. A thermometer is an example of an object that illustrates an interval scale.
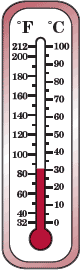
Each mark on the thermometer above shows a specific interval. On the left of the thermometer, with the exception of the freezing point (32°F) and boiling point (212°F) of water, the thermometer shows intervals of 20°F. The difference between 20°F and 40°F is the same as the difference between 40°F and 60°F. On the Celsius side of the thermometer, it increases from 0°C to 100°C in intervals of 10°C.
Ratio scale
The ratio scale is the fourth level of measurement scale. It is an extension of the interval scale with the key addition being the absolute zero (or true zero) property. The absolute zero property gives meaning to 0 on the scale in that a measurement of 0 means that the characteristic being measured is not present. Weight, as would be measured by the scale below, is an example of data on a ratio scale. A weight of 0 on the scale below means that there is 0 weight, or nothing on the scale.
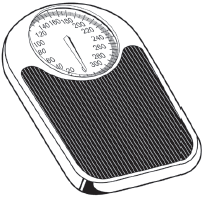
Other examples of data on a ratio scale include height, age, the amount of money a person is carrying, and more. A person who is 0 feet tall, is 0 years old, or who has $0 are all data that fall under the ratio scale, since those 0's all have significance.
In contrast, a temperature of 0°C on a thermometer does not have the same meaning in that it is just another measurement of temperature. It may have significance as a temperature at which something eventful happens (water freezes), but from the perspective of measurement scale, it is just another temperature, and does not exhibit the absolute zero characteristic. It is therefore on the interval, not the ratio scale.
