Area of a hexagon

The area of a hexagon is the space contained within its perimeter. The grey space is the area of the hexagon in the figure below.

Area formula of a regular hexagon

There are many different types of hexagons. The most common type is a regular hexagon, which is a hexagon that has sides of equal length and angles of equal measure.

The area, A, of a regular hexagon can be found given only its side length, s, with the formula:

Sometimes, in real life, it is easier to measure the distance between opposite sides of a regular hexagon. In such a case, the area of the hexagon is:

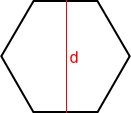
The apothem, a, of a regular hexagon is half of the distance between opposite sides of the hexagon. The area formula using the apothem is:

Finding area using a grid

Another way to find the area of a hexagon is to determine how many unit squares it takes to cover its surface. Below is a unit square with side lengths of 1 cm.

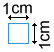
A grid of unit squares can be used when determining the area of a hexagon.

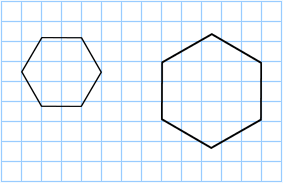
The grid above contains unit squares that have an area of 1 cm² each. The regular hexagon on the left contains 6 full squares and 10 partial squares, so it has an area of approximately:

The regular hexagon to the right contains 17 full squares and 10 partial squares, so it has an area of approximately:

This method can be used to find the area of any shape; it is not limited to regular hexagons. However, it is only an approximate value of the area. The smaller the unit square used, the higher the accuracy of the approximation. Using a grid made up of 1 mm squares is 10 times more accurate than using a grid made up of 1 cm squares.

Derivation of the area formula

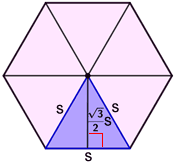
Divide the regular hexagon into six equilateral triangles by drawing line segments to opposite vertices. Each triangle has a side length s and height (also the apothem of the regular hexagon) of . The area, A, of one of the equilateral triangles, drawn in blue, can be found using:

Since there are six equilateral triangles, the area of a regular hexagon is: