Area and perimeter
Area and perimeter are two commonly discussed measurements of 2D figures (plane figures).
Area
The area of a figure is a measurement of the amount of space the figure takes up. Another way to think of area is as the measure of the space enclosed by a figure. For example, the area of a square is made up of the space between each side of the square. The figure below depicts area as the shaded portion (everything inside the sides of the square) of the square:

The area of a square is calculated as the product of its length and width, which are the same. Using the figure above, the area of the square is 5 × 5 = 25. When the unit of measure is not known, it is common practice to describe area in terms of "square units." Thus, the square above has an area of 25 square units. Commonly used measures of area include square feet (ft2), square meters (m2), square miles (mi2), and so on.
Calculating area
There are a number of different ways to calculate the area of geometric figures. For example, there are well-defined area formulas for simple shapes such as squares, triangles, circles, and more. Depending on the known information, calculating the area of a figure can be as simple as plugging information into a formula. Visit the area formula page to reference the area formulas for a number of simple shapes.
For complex shapes that are made up of simple shapes, the total area can be determined as the sum of the areas of the simple shapes that comprise it. For example, the figure below is made up of a square and a right triangle.

The area of the square, as calculated above, is 25 square units. The area of the triangle can be determined as A = ½bh, where b is the base and h is the height:
½(5)(8) = 20
The total area is therefore:
25 + 20 = 45 square units
Area can also be determined using the concept of unit squares. A unit square is a square with side lengths of 1 such that the area of the square is 1 square unit. The total area of a figure can be determined by counting the number of unit squares that fit within the figure; this can be exact depending on the figure, and if not, unit squares can still be used to approximate the area.
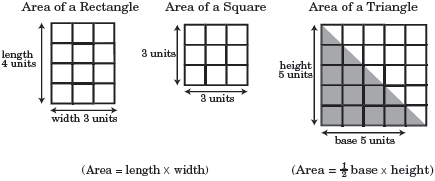
The areas of the figures above can be determined by counting unit squares or by using their respective area formulas. In either case, their areas will be the same; the area of the rectangle is 12 square units; the area of the square is 9 square units, and the area of the triangle is 12.5 square units.
Perimeter
In geometry, the perimeter of a figure is the distance around it. Visit the perimeter page to reference the formulas for the perimeters of some basic 2D figures.
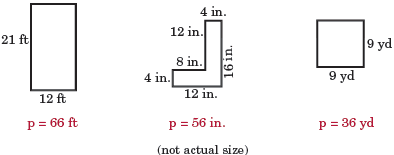
Briefly, for a polygon, the perimeter is the sum of the sides of the polygon. For example, for a square, the perimeter is the sum of its 4 sides; for a triangle, it is the sum of its 3 sides, and so on. The perimeters of the following figures are all determined by summing each side of the figure:
Curved figures, such as circles, also have perimeters. In the case of a circle, the perimeter is instead referred to as the circumference of the circle. Calculating the perimeter of curved surfaces, particularly irregular ones, can be a lot more difficult than calculating the perimeter of shapes made up of line segments. The perimeter of many common curved shapes (such as circles) can be found using known formulas. For less regular figures, more complicated mathematics is necessary. One way to measure the perimeter of curved figures in a real-world setting is to use some string or rope to form the outline of the shape then measure the length of string required to outline the shape. However, depending on the size of the figure, as well as other factors, this may not be possible.
