Perimeter
The perimeter is the total length or distance around a two dimensional shape. In the figure below, the perimeter of each shape is the sum of the lengths of each side, shown in red. The perimeter of a circle or ellipse is called the circumference. For a polygon, the perimeter is the sum of its side lengths.
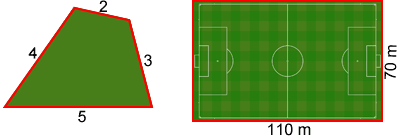
The perimeter of the quadrilateral above is 2 + 3 + 4 + 5 = 14. The perimeter of the soccer field above is 110 + 110 + 70 + 70 = 360 meters. To add a fence around the edges of the entire soccer field, the fence would have to cover 360 meters.
Perimeter of common geometric figures
Below are formulas for the perimeters of some common geometric figures.
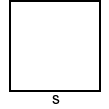
Square
The perimeter of a square with side length s is:
P = 4s
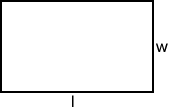
Rectangle
The perimeter of a rectangle with length, l, and width, w, is.
P = 2l + 2w
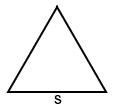
Equilateral triangle
The perimeter of an equilateral triangle with side lengths s is:
P = 3s
Regular polygon
The perimeter of a regular (all sides are equal) n-sided polygon with side lengths s is:
P = ns
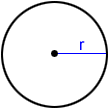
Circle
The circumference of a circle with radius r is:
C = 2πr
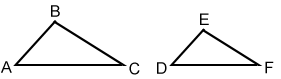
Perimeter of similar figures
If geometric figures are similar, the ratio of their perimeters is equal to the ratios of their corresponding sides. For the similar triangles ABC and DEF below,
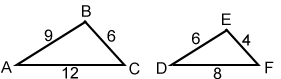
Example:
Show that the ratio of the perimeters of the two similar triangles below is equal to the ratios of their corresponding sides.
Distance formula
Given the coordinates of the vertices of a polygon in the coordinate plane, the side length of the polygon can be calculated using the distance formula:
where d is the distance between the two points with coordinates (x1, y1) and (x2, y2). Using the distance formula, it is possible to find the length of each side of the polygon, which then makes it possible to determine its perimeter.
Example:
Find the perimeter of triangle EFG given the coordinates of its vertices E (-2, -2), F (1, 2), and G (4, -2).
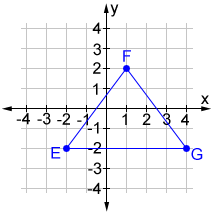
The perimeter of the triangle is EF + FG + EG, the lengths of which can be found using the distance formula:
| P = 5 + 5 + 6 = 16 |
