Area of a parallelogram
The area of a parallelogram is the space contained within its perimeter. The gray space is the area of the parallelogram in the diagram below.
Area formula of a parallelogram
Area formula using the base and height
The area of a parallelogram is the product of the length of its base (b) and height (h).
A = b×h
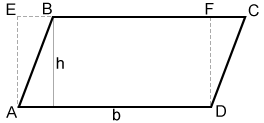
In the diagram above, △ABE ≅ △DCF. Therefore, the area of parallelogram ABCD is equal to the area of rectangle AEFD, or b×h.
Area formula using the sides and angle
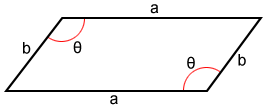
If the side lengths and an angle of a parallelogram are given, the area is:
A=a·b·sin(θ)
where a and b are the lengths of the adjacent sides and θ is one of the angles.
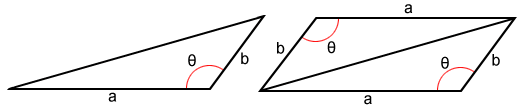
The area of a triangle with angle θ between sides a and b is . A diagonal of a parallelogram divides it into two congruent triangles, so the area of a parallelogram is twice the area of either of those triangles. Using the area formula for a triangle, the area of the parallelogram shown above is:
Example:
Find the area of a parallelogram to the nearest whole number.
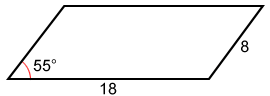
A = 18 · 8 · sin(55°) ≈ 118
Finding area using a grid
Another way to find the area of a parallelogram is to determine how many unit squares it takes to cover its surface. Below is a unit square with side length 1 cm.
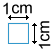
A grid of unit squares can be used when determining the area of a parallelogram.
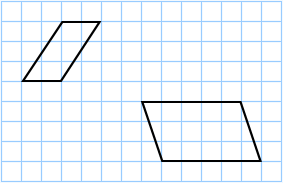
The grid above contains unit squares that have an area of 1 cm2 each. The parallelogram on the left contains 2 full squares and 8 partial squares, so it has an area of approximately:
The parallelogram to the right contains 12 full squares and 6 partial squares so it has an area of approximately:
This method can be used to find the area of any shape; it is not limited to parallelograms. However, it is only an approximate value of the area. The smaller the unit square used, the higher the accuracy of the approximation. Using a grid made up of 1 mm squares is 10 times more accurate than using a grid made up of 1 cm squares.
