Equilateral triangle
An equilateral triangle is a triangle that has sides that are all equal in length.
An isosceles triangle has at least two equal sides, so an equilateral triangle is also an isosceles triangle.
Angle measures
An equilateral triangle is also called an equiangular triangle since its three angles are equal to 60°.
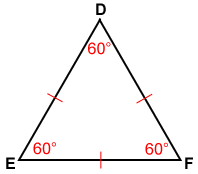
In an isosceles triangle, the base angles are congruent. Recall from above that an equilateral triangle is also an isosceles triangle. Since DE≅EF, the base angles, ∠D and ∠F, are congruent. Also, since DE≅DF, ∠E≅∠F, so by the transitive property, ∠D≅∠E≅∠F.
Since the sum of the angles for any triangle is 180°:
This is true for any equilateral triangle.
Properties of equilateral triangles
Equilateral triangles are regular polygons
Since an equilateral triangle is also an equiangular triangle, it is a regular polygon.
All equilateral triangles are similar
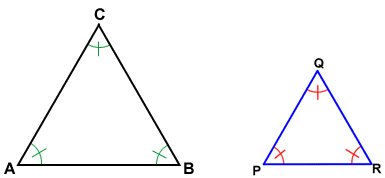
Triangle △ABC and triangle △PQR are equiangular so, △ABC ~ △PQR.
Altitudes of equilateral triangles
An altitude of an equilateral triangle is also an angle bisector, median, and perpendicular bisector. The three altitudes of an equilateral triangle intersect at a single point.
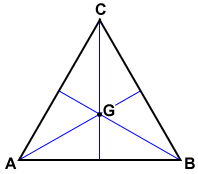
The three altitudes extending from the vertices A, B, and C of △ABC above intersect at point G. Since the altitudes are the angle bisectors, medians, and perpendicular bisectors, point G is the orthocenter, incenter, centroid, and circumcenter of the triangle.
Lines of symmetry of an equilateral triangle
The three altitudes of an equilateral triangle are also lines of symmetry. Refer to altitude BD extending from vertex B in the diagram below:
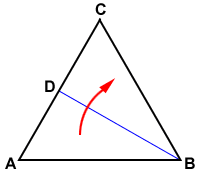
Side AB reflects across the altitude to side BC. Similarly, side BC reflects to side AB. Side AC reflects onto itself when reflecting across the altitude. The same relationships would be found for altitudes drawn from vertices A and C.
Special triangles
An altitude divides an equilateral triangle into two 30°-60°-90° triangles.
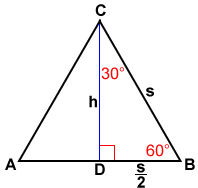
Altitude CD divides equilateral triangle △ABC into two 30°-60°-90° triangles. Triangles △ACD and △BCD both have legs of length , and hypotenuse s.
