Area of a rhombus
The area of a rhombus is the space contained within its perimeter. A rhombus is a parallelogram in which all sides are congruent. The grey space is the area of the rhombus in the diagram below.
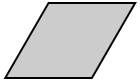
Area formula
There are several formulas that can be used to find the area of a rhombus depending on the known parameters.
Using diagonals
The area, A, of a rhombus is half the product of its two diagonals.
where d1 and d2 are the lengths of the two diagonals.
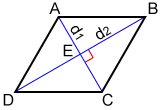
Referencing rhombus ABCD above, Let AC = d1 and BD = d2. The diagonals of a rhombus are perpendicular to each other, so AC⟂ DB. Rhombus ABCD can be decomposed into triangles ABC and ADC.
The area of △ABC = where BE is the altitude of △ABC. The area of △ADC =
where DE is the altitude of △ADC. The area of rhombus ABCD equals the sum of the areas of △ABC and △ADC.
| △ABC + △ADC = | |
| = | |
| = | |
| = |
Example:
If the area of a rhombus is 230, and one of its diagonals is 10, what is the length of the other diagonal?
Let d1 = 10. Since A = 230 we can find d2 as follows:
230 = 5 × d2
d2 = 46
Using side and height
Since a rhombus is also a parallelogram, we can use the formula for the area of a parallelogram:
A = b×h
where b is the base or the side length of the rhombus, and h is the corresponding height.
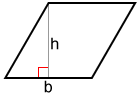
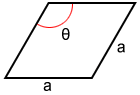
Using side and angle
If the side length and one of the angles of the rhombus are given, the area is:
A = a2 × sin(θ)
where a is side length and θ is one of the angles.
Finding area using a grid
Another way to find the area of a rhombus is to determine how many unit squares it takes to cover its surface. Below is a unit square whose dimensions are 1 cm.
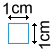
A grid of unit squares can be used when determining the area of a rhombus.
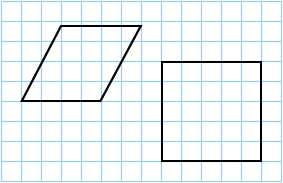
The grid above contains unit squares that have an area of 1 cm2 each. The rhombus on the left contains 8 full squares and 12 partial squares, so it has an area of approximately:
The rhombus to the right contains 25 full squares, so it has an area of approximately 25 cm2.
This method can be used to find the area of any shape; it is not limited to rhombuses. However, it is only an approximate value of the area. The smaller the unit square used, the higher the accuracy of the approximation. Using a grid made up of 1 mm squares is 10 times more accurate than using a grid made up of 1 cm squares.
