Area formula
The area of a two dimensional shape or geometric figure is the space contained within its perimeter.
Area formulas of common shapes
The exact area of many common shapes can be calculated using well-defined formulas.
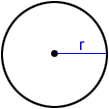
Circle
The area of a circle with radius r is:
A = πr2
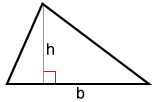
Triangle
The area of a triangle with base, b, and height, h, is:
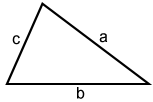
If the side lengths of the triangle are given, the area can be found using:
where a, b, and c are side lengths, and
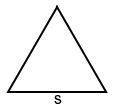
Equilateral triangle
The area of an equilateral triangle with side length, s, is:
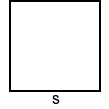
Square
The area of a square with side, s, is:
A = s2
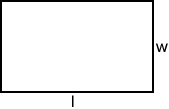
Rectangle
The area of a rectangle with length, l, and width, w, is:
A = lw
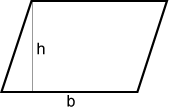
Parallelogram
The area of a parallelogram with base, b, and height, h, is:
A = bh
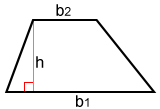
Trapezoid
The area of a trapezoid with bases, b1 and b2, and height, h, is:
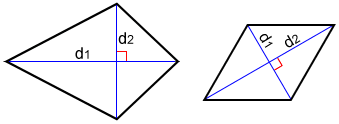
Kite and Rhombus
The area of a kite, or rhombus, with diagonal length d1 and d2 is:
Regular hexagon
The area of a regular hexagon with side length s is:
Regular pentagon
The area of a regular pentagon with side length s is:
Regular octagon
The area of a regular octagon with side length s is:
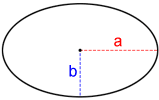
Ellipse
The area of an ellipse with semi-major axis, a, and semi-minor axis, b, is:
A = πab
Area of a composite figure
Many geometric figures are made up of two or more common figures, and their areas can be calculated using a combination of the area formulas above. These types of geometric figures are referred to as composite figures.
Example:
Find the area of the composite figure below to the nearest tenth. The figure is composed of an equilateral triangle, a rectangle, and a semi-circle (half of a circle).
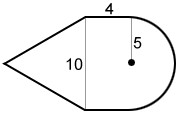
Using the formula for the area of an equilateral triangle and side length 10:
The length and width of the rectangle are 10 in and 4 in respectively, so its area is
A = 10×4 = 40
The area of the semi-circle is one-half the area of a circle. The semi-circle has a radius of 5 and its area can be found by halving the area formula of a circle:
The total area of the composite figure is the sum of all its parts:
A = 86.6 + 40 + 39.3 = 122.6
