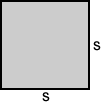
Area of a square
The area of a square is the space contained within its perimeter. The grey space in the figure below is the area of the square.

Formula for the area of a square
There are several formulas that can be used to find the area of a square.
Using side length
The area, A, of a square with side length s is:
A = s2
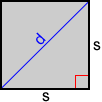
Using diagonals
Given the diagonal of a square, the following formula can be used:
where d is the length of the diagonal.
Derivation
Find the length of the diagonal in terms of s. The diagonal of a square divides the square into two congruent right triangles which allows us to use the Pythagorean Theorem to find the length of d in terms of s:
s2 + s2 = d2
2s2 = d2
Example:
The area of the region between the two squares (the area shaded in green), is 144. If the distance between the outer and inner sides of the squares is 2, what is the area of the outer square?
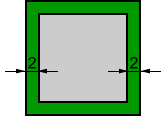
Let x be the side length of the inner (grey) square. This makes the side length of the outer square x + 4.
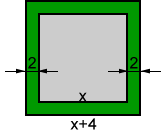
The area of the region shaded in green is equal to the difference between the area of the outer square and inner square. Using this relationship, we can solve for x:
144 = (x + 4)2 - x2
144 = x2 + 8x + 16 - x2
128 = 8x
x = 16
Substituting x into x + 4, the length of the side of the outer square is 16 + 4, so:
A = 202 = 400
