Triangle
A triangle is a 3-sided polygon.
Parts of a triangle
All triangles are made up of three sides and three angles. The point at which two sides of a triangle meet is referred to as a vertex. Triangles are commonly labeled at their vertices, as shown in the figure below:
The three sides for triangle ABC shown above, written symbolically as △ABC, are line segments AB, BC, and AC. A is formed when two sides of a triangle intersect. △ABC has vertices at A, B, and C. An interior angle is formed at each vertex. Angles A, B, and C are the three interior angles for △ABC.
A line segment from a vertex of a triangle to the side opposite the vertex that is perpendicular to the opposite side is called an altitude. The side that is perpendicular to the altitude is called the base of the triangle. In triangle ABC below, line segment CD is an altitude, and side AB is a base.
It is common to name the sides of a triangle based on its opposing angle. This often involves the use of upper-case and lower-case letters to name an angle and its opposing side. Refer to △ABC above as an example. Side BC is opposite of angle A, so it is labeled as side a.
Types of triangles
Triangles are often classified by their angles and sides, as shown in the tables below.
By angles:
| Type | Angles | Figure |
|---|---|---|
| Acute | all interior angles < 90° |  |
| Obtuse | 1 interior angle > 90° |  |
| Right | 1 angle = 90° |  |
| Equiangular | each interior angle = 60° |  |
By sides:
| Type | Sides | Figure |
|---|---|---|
| Scalene | no 2 sides are congruent |  |
| Isosceles | 2 congruent sides |  |
| Equilateral | all sides are congruent |  |
Triangle properties
Below are some triangle properties worth noting.
Angle sum
Using properties of parallel lines and alternate interior angles, we can show the sum of the interior angles for a triangle is 180°.
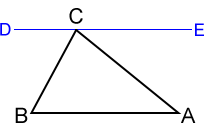
- For △ABC shown above, let line DE, containing vertex C, be parallel to side AB. Since ∠DCE is a straight angle, ∠ECA + ∠DCB + ∠BCA = 180°.
- Also, since DE is parallel to AB, this forms two sets of congruent alternate interior angles such that ∠ECA≅∠A and ∠DCB≅∠B.
- Substituting angles A and B into our previous equation, ∠A + ∠B + ∠BCA = 180°, where ∠BCA = ∠C.
Exterior angles
For a triangle, an exterior angle is an angle formed by one side of the triangle and a line extended from another of its sides. The measure of an exterior angle of a triangle equals the sum of its two remote interior angles.
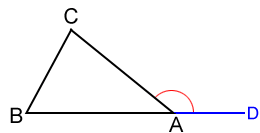
For △ABC shown above, ∠CAD is the exterior angle for ∠A and ∠B and ∠C are the two remote interior angles. We know that ∠CAB + ∠B + ∠C = 180°. Also, ∠CAB and ∠CAD form a straight angle, so ∠CAB + ∠CAD = 180°. Since both sums equal 180°:
∠CAB + ∠CAD = ∠CAB + ∠B + ∠C
∠CAD = ∠B + ∠C
The same can be shown for any exterior angle of any triangle.
Comparing sides and angles
A triangle can only be formed when the sum of any two sides of the triangle is greater than its third side.
Example:
The sides of △ABC are a = 4, b = 6, and c = 9. Can a triangle be formed with the given sides?
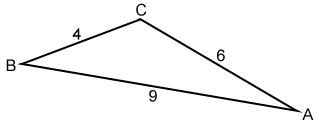
Since 4 + 6 > 9, 4 + 9 > 6, and 6 + 9 > 4 we can form △ABC. This only tells us that a triangle can be formed by the three given sides. It does not classify the triangle.
If one side of a triangle is longer than another side, the angle opposite the longer side must be greater than the angle opposite the smaller side. This is true for any triangle.
As an example, you can see from the side and angle measures given for △ABC above, AB > BC. Based on this, we know that ∠C > ∠A.
Conversely, the greater the angle measure, the greater the length of the opposite side. Since ∠B > ∠A, AC > BC.