Congruent triangles
Two or more triangles that have the same size and shape are called congruent triangles.
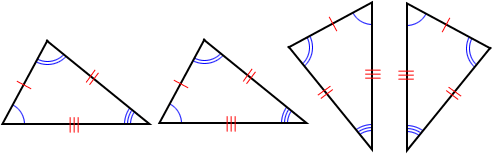
The four triangles are congruent with each other regardless whether they are rotated or flipped. The congruence of two objects is often represented using the symbol "≅". In the figure below, △ABC ≅ △DEF.
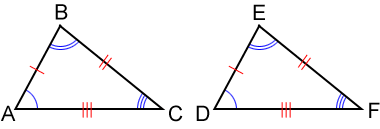
As shown in the figure above, the lengths of the corresponding sides and measures of the corresponding angles do not have to be explicitly shown to indicate congruence. An equal number of tick marks can be used to show that sides are congruent. Similarly, an equal number of arcs can be used to show that angles are congruent.
The corresponding congruent angles are: ∠A≅∠D, ∠B≅∠E, ∠C≅∠F.
The corresponding congruent sides are:
≅, ≅, ≅.
Also, the corresponding vertices of the two triangles should be written in order. So, △ABC≅△DEF could also be written as △CBA≅△FED but not △BCA≅△DEF.
Determining congruence for triangles
Two triangles must have the same size and shape for all sides and angles to be congruent, Any one of the following comparisons can be used to confirm the congruence of triangles.
Side-Side-Side (SSS)
If three sides of one triangle are congruent to three sides of another triangle, the two triangles are congruent.
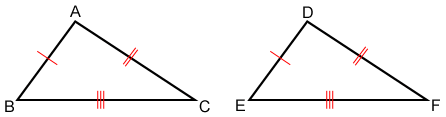
In the figure above, ≅, ≅, ≅. Therefore △ABC≅△DEF.
Side-Angle-Side (SAS)
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the two triangles are congruent.
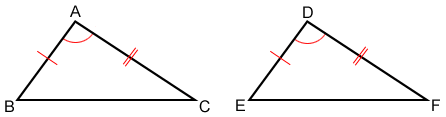
In the figure above, ≅, ≅, and ∠A≅∠D. Therefore, △ABC≅△DEF.
Angle-Side-Angle (ASA)
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the two triangles are congruent.
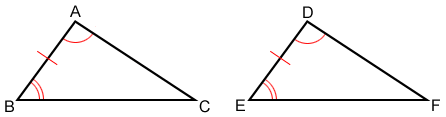
In the figure above, ∠A≅∠D, ∠B≅∠E, and ≅.Therefore,△ABC≅△DEF.
Angle-Angle-Side (AAS)
If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle, the two triangles are congruent.
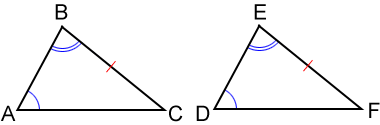
In the figure above, ∠D≅∠A, ∠E≅∠B, and ≅. Therefore, △DEF≅△ABC.
The Angle-Angle-Side theorem is a variation of the Angle-Side-Angle theorem. In the figure, since ∠D≅∠A, ∠E≅∠B, and the three angles of a triangle always add to 180°, ∠F≅∠C. This then becomes an Angle-Side-Angle comparison since ∠E≅∠B, ∠F≅∠C, and ≅.
Hypotenuse-Leg congruence
If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another triangle, the two triangles are congruent.
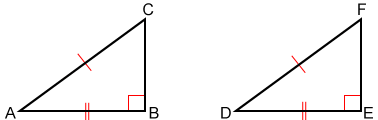
In the figure above, ≅, ≅, ∠B and ∠E are right angles. Therefore, △ABC≅△DEF.
Angle-Side-Side (ASS)
If two sides and the non-included angle of one triangle are congruent to two sides and the non-included angle of another triangle, the two triangles are not always congruent.
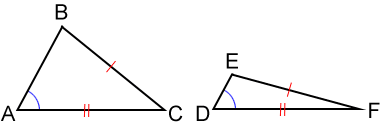
In the figure above, ≅, ≅, ∠A≅∠D, but △ABC is not congruent to △DEF.
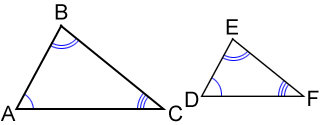
Angle-Angle-Angle (AAA)
If three angles of one triangle are congruent to three angles of another triangle, the two triangles are not always congruent. As shown in the figure below, the size of two triangles can be different even if the three angles are congruent.
Corresponding parts
When two triangles are congruent, all their corresponding angles and corresponding sides (referred to as corresponding parts) are congruent.
Once it can be shown that two triangles are congruent using one of the above congruence methods, we also know that all corresponding parts of the congruent triangles are congruent (abbreviated CPCTC).
Example:
State the congruence for the two triangles as well as all the congruent corresponding parts.
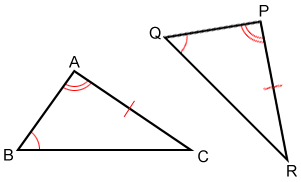
Since two angles of △ABC are congruent to two angles of △PQR, the third pair of angles must also be congruent, so ∠C≅∠R, and △ABC≅△PQR by ASA.
The corresponding congruent angles are: ∠A≅∠P, ∠B≅∠Q, ∠C≅∠R.
The corresponding congruent sides are: ≅, ≅, ≅.
