Pythagorean Theorem

The Pythagorean Theorem shows the relationship between the sides of a right triangle. It states that for a right triangle, the sum of the areas of the squares formed by the legs of the triangle equals the area of the square formed by the triangle's hypotenuse. This is expressed as:

a² + b² = c²

where a and b are the legs of a right triangle and c is the hypotenuse.

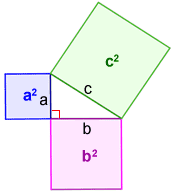
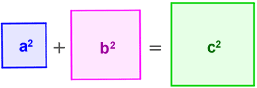
The Pythagorean Theorem is named after the Greek mathematician Pythagoras. It is one of the most well-known theorems in mathematics. Based on the Pythagorean Theorem:

The length of the hypotenuse is .

The lengths of legs a and b are and .

Example:

For a right triangle, hypotenuse c = 10 and leg a = 6. Find the length of leg b.

b =
=
=
=	8

Pythagorean Theorem proof

There are many ways to prove the Pythagorean Theorem. One way to do so involves the use of the areas of squares and triangles.

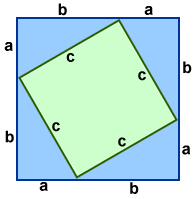
• The green square is inscribed in the blue square above, creating four congruent right triangles with legs a and b, and hypotenuse c.
• The sides of the blue square are each (a + b), therefore the area of the blue square is (a + b)².
• The area of the blue square also equals the area of the green square plus the area of the 4 right triangles around it. The area of the green square is c² and the area of each of the right triangles is . Therefore, the area of the blue square is equal to .
• Setting the formulas for the area of the blue square equal:
  (a+b)² = c² + 2ab
  a² + 2ab + b² = c² + 2ab
  a² + b² = c²

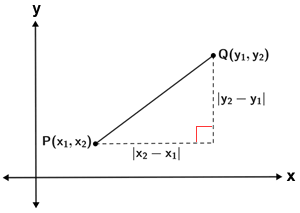
Coordinate geometry

In the coordinate plane, the distance between two points can be found using the Pythagorean Theorem.

In the figure below, the distance between P and Q is,