45-45-90 triangle
A 45-45-90 triangle is a right triangle having interior angles measuring 45°, 45°, and 90°.
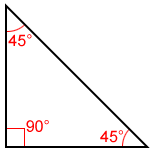
A 45-45-90 triangle is also an isosceles triangle, which means its two legs are equal in length.
Similarity
All 45-45-90 triangles are similar.
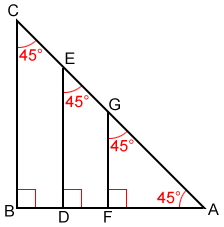
Line segments DE and FG are perpendicular to side AB of the 45-45-90 triangle, ABC. Triangles ADE and AFG are also 45-45-90 triangles so, △ABC~△ADE~△AFG.
45-45-90 triangle side lengths
The ratio of the side lengths of a 45-45-90 triangle are:
- The legs opposite the 45° angles (the shorter sides) are
of the length of the hypotenuse (the side opposite the 90° angle)
- The hypotenuse is
times the length of either leg.
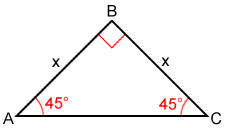
Since a 45-45-90 triangle is also an isosceles triangle, the two legs are equal in measure. Assuming x is the length of the leg and b is the length of the hypotenuse and using the Pythagorean Theorem:
x2 + x2 = b2
Thus, the ratio of the side lengths of a 45-45-90 triangle are or
respectively.
Example:
Find the lengths of the legs for △PQR below.
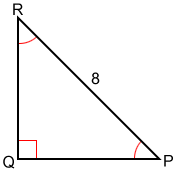
△PQR is a 45-45-90 triangle since ∠P≅∠R and ∠Q=90°. Sides PQ and QR are of the length of PR:
45-45-90 triangle in trigonometry
In the study of trigonometry, the 45-45-90 triangle is considered a special triangle. Knowing the ratio of the sides of a 45-45-90 triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angle 45°.
For example, sin(45°), read as the sine of 45 degrees, is the ratio of the side opposite the 45° angle of a right triangle, to its hypotenuse.
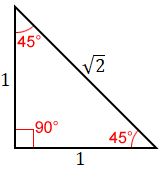
Using the side lengths , for the 45-45-90 triangle above:
Similarly:
tan(45°) = 1
