Obtuse triangle
An obtuse triangle is a triangle that has one angle that has a measure greater than 90° but less than 180°. The other two angles in the triangle are acute angles (< 90°).
What is an obtuse triangle
An obtuse triangle is a type of triangle characterized by having one interior angle that measures larger than 90°. The remaining two angles must be acute because a triangle's interior angles always sum to 180°. The other types of triangles are acute, right, equilateral, scalene, and isosceles triangles.
Obtuse triangle definition
An obtuse triangle is a 3-sided polygon in which one of the interior angles measures greater than 90° but less than 180°. The other two angles in the triangle measure less than 90°, and the sum of the 3 angles must equal 180°. An example of an obtuse triangle in real life is part of the roof of a house, as shown in the figure below.

It is possible for an obtuse triangle to be scalene or isosceles, but it cannot be right, equilateral, or acute.
Types of triangles
There are two different types of obtuse triangles: isosceles and scalene.
Isosceles obtuse triangle
An isosceles obtuse triangle has two sides of equal length and one much longer side that is opposite the largest interior angle of the triangle. The figure below shows an isosceles obtuse triangle.

Scalene obtuse triangle
A scalene triangle is a triangle in which none of the sides have equal length. A scalene obtuse triangle is a one in which none of the sides have equal length and one of the internal angles measures greater than 90°. The figure below shows a scalene obtuse triangle.

Obtuse triangle properties
Below are some properties of obtuse triangles:
- One interior angle of an obtuse triangle measures between 90° and 180°. The other two interior angles measure less than 90° and the sum of the three interior angles is 180°.
- The orthocenter and circumcenter of an obtuse triangle lie outside of the triangle. Its incenter and centroid lie inside the triangle. These points are referred to as points of concurrency of a triangle.
- Given sides a, b, and c, where c is the longest side of an obtuse triangle: c2 > a2 + b2. In other words, the square of the longest side of an obtuse triangle is always greater than the sum of the squares of its shorter sides.
- The side opposite the largest angle measure is the longest side of the triangle.
- A triangle cannot be both obtuse and right (or acute). An obtuse triangle also cannot be equilateral.
Properties of triangles
Below are properties of all triangles.
- A triangle is a polygon with 3 sides, 3 angles, 3 vertices.
- The lengths of the sides of a triangle correspond to the measures of their angles; the larger the angle, the larger the side; the smaller the angle, the smaller the side. The longest side of a triangle is opposite the angle with the largest measure and the shortest side of the triangle is opposite the smallest angle.
- Angle sum property - The sum of the interior angles of a triangle is always equal to 180°. The sum of the exterior angles of a triangle is always equal to 360°
- Triangle inequality - The sum of the lengths of two sides of a triangle is always larger than the length of the third side; the difference between the lengths of any two sides is less than the length of the third side.
- Exterior angle theorem - The measure of an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles of the triangle.
- Congruent - Two triangles are congruent if all of their corresponding sides and angles are equal.
- Similar - Two triangles are similar if all their corresponding angles are equal and their corresponding sides have the same ratio. In other words, the shape of the triangle is identical, but the size of the triangles are different.
- The sum of consecutive interior and exterior angles of a triangle is supplementary (180°).
Triangle formulas
Below are some formulas related to obtuse triangles.
Perimeter of an obtuse triangle
The perimeter of an obtuse triangle is the sum of lengths of its sides. Given a triangle with sides a, b, and c, the perimeter is:
P = a + b + c
There are many different ways to find the lengths of the sides of a triangle given enough information. If the side lengths are known, the perimeter is straightforward to calculate.
Area of an obtuse triangle
There are a number of different ways to find the area of an obtuse triangle. The typical triangle area formula is
where b is the base and h is the height of the triangle. Any side of the triangle can be chosen as the base; the height for an obtuse triangle can be found by extending the base and drawing the altitude from the vertex outside the triangle down to the extended base. Refer to the figure below.

Heron's formula
Heron's formula is a formula for the area of a triangle given that all 3 sides of the triangle are known. Heron's formula for the area of a triangle is
where a, b, and c are the sides of the triangle and s is the semiperimeter of the triangle which is found as:
Converse of the Pythagorean theorem
For a right triangle with hypotenuse of length c, and legs of lengths a and b, the Pythagorean Theorem states:
a2 + b2 = c2
For any triangle, if a2 + b2 < c2, where c is the longest side, the triangle is an obtuse triangle.
Example:
Is triangle △ABC an obtuse triangle?
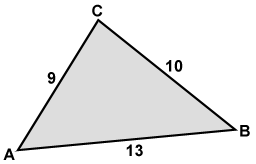
Side AB above is the longest side. Plugging this into the Pythagorean Theorem where c = 9 and a and b = 6:
a2 + b2 = 62 + 62 = 72
c2 = 92 = 81
72 < 81
Since a2 + b2 < c2, △ABC is an obtuse triangle with obtuse angle C.


