Right triangle
A right triangle is a triangle in which one angle has a measurement of 90° (a right angle), such as the triangle shown below.
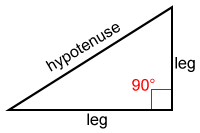
Right angles are typically denoted by a square drawn at the vertex of the angle that is a right angle. The side opposite the right angle of a right triangle is called the hypotenuse. The sides that form the right angle are called legs. The hypotenuse is the longest side of the right triangle.
Since the measure of a right angle is 90°, and since the sum of the three angles in any triangle equals 180°, the sum of the other two angles in a right triangle must be 180° - 90° = 90°, so they must be acute angles. Otherwise, the shape cannot be a triangle.
Right triangles and the Pythagorean Theorem
The Pythagorean Theorem, named after the Greek mathematician Pythagoras, is one of the more well-known theorems in mathematics. The theorem shows a distinct relationship between the sides of a right triangle which can be expressed as:
a2 + b2 = c2
where a and b are the lengths of the two legs, and c is the length of the hypotenuse of the right triangle.
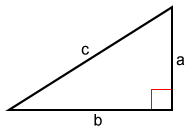
The sets of positive integers that satisfy the Pythagorean Theorem equation are called Pythagorean triples. If a triangle has side lengths such that the set of sides comprise a Pythagorean triple, the triangle is a right triangle. Also, if the side lengths of a right triangle are all integers, they are a set of Pythagorean triples.
For example, if a = 3, b = 4, and c = 5, then:
32 + 42 = 9 + 16 = 25 = 52
So, the Pythagorean Theorem is satisfied and 3-4-5 is a set of Pythagorean triples.
There are many sets of Pythagorean triples. Examples include 5-12-13, 6-8-10, 7-24-25, 9-12-15, 9-40-41.
Right triangles in trigonometry
Right triangles are widely used in trigonometry. In trigonometry, the legs of a right triangle are often referred to as the opposite side and the adjacent side of their respective acute angle, θ, as shown in the figure below.
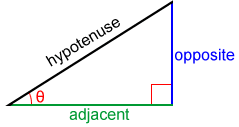
Trigonometric functions are often defined in terms of right triangles as:
Inscribed right triangle
If a right triangle is inscribed in a circle, one of its sides (the hypotenuse) is a diameter of the circle. Conversely, if the diameter of a circle forms one of the sides of an inscribed triangle, the inscribed triangle is a right triangle.
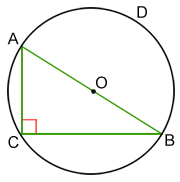
Right triangle ABC shown above with hypotenuse AB is inscribed in circle O. The measure of an arc is twice that of the angle it subtends anywhere on the circle's circumference, so arc ADB is twice the measure of right angle ACB.
arc ADB = 2 × 90° = 180°
A central angle of a circle is an angle that has its vertex at the center of the circle and whose legs are radii that intersect the circle at two distinct points. The measure of an arc is equal to the measure of the central angle that intercepts it. Angle AOB is a central angle of the circle above and intercepts arc ADB at points A and B. Based on this, we know that angle AOB measures 180°, making it a straight angle. Any circle measures a total of 360°, so arc ADB comprises half of the circle, meaning that line segment AB divides the circle in half, confirming that the hypotenuse of right triangle ABC is a diameter of the circle.
