Types of triangles
A triangle is a three-sided polygon that has an interior angle at each of its vertices. Triangles are often classified by their angles or sides.
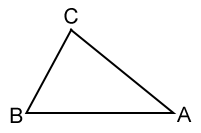
Triangle △ABC, shown above, has sides AB, BC, and AC, and angles A,B,and C, formed at vertices A, B, and C.
Triangles classified by their angles
The following table shows the types of triangles classified by their angles.
| Type | Angles | Figure |
|---|---|---|
| Acute | all interior angles < 90° | 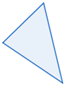 |
| Obtuse | 1 interior angle > 90° |  |
| Right | 1 angle = 90° |  |
| Equiangular | each interior angle = 60° | 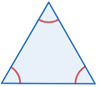 |
Triangles classified by their sides
The following table shows the types of triangles classified by their sides.
| Type | Sides | Figure |
|---|---|---|
| Scalene | no 2 sides are congruent |  |
| Isosceles | 2 congruent sides | 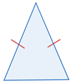 |
| Equilateral | all sides are congruent | 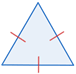 |
Using the Pythagorean Theorem to classify triangles by their angles
When one of the angles in a triangle is a right angle, the triangle is a right triangle. The lengths of the three sides of a right triangle follow Pythagorean Theorem. The Pythagorean Theorem can also be used to classifies triangles by angles as follows:
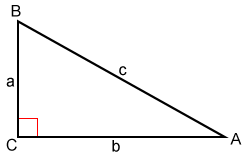
For △ABC, given that side c is the longest side:
- If c2 = a2 + b2, then △ABC is a right triangle with right angle C.
- If c2 > a2 + b2, then △ABC is an obtuse triangle with obtuse angle C.
- If c2 < a2 + b2, then △ABC is an acute triangle with all angles acute.
Example:
Classify a triangle that has side lengths 3, 6, and 8.
Since 8 is the largest side length, let c = 8, a = 3, and b = 6:
| c2 = 82 = 64 |
| a2 + b2 = 32 +62 = 9 + 36 = 45 |
Since 64 > 45, c2 > a2 + b2, so the triangle is an obtuse triangle.
