Pentagon
A pentagon is a five-sided polygon.
What is a pentagon
In geometry, a pentagon is a closed 2D shape that has 5 sides and 5 angles.
Pentagon shape
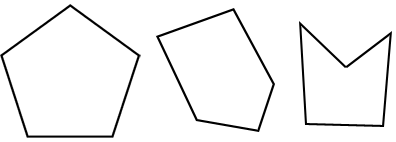
A pentagon is a five-sided polygon; there are a few different pentagon shapes. The figure below shows 3 examples of what a pentagon looks like:
One famous example of a pentagon is The Pentagon, near Washington, D.C.; it is one of the world's largest office buildings and it is in the shape of a pentagon. The figure below shows an aerial view of The Pentagon, outlined in red.

Types of pentagons
Pentagons are classified as either regular or irregular and concave or convex.
Regular pentagon and irregular pentagon
Like other polygons, a pentagon can be classified as regular or irregular.
- Regular pentagon - all sides and interior angles are equal.
- Irregular pentagon - not all sides and interior angles are equal.
The figure below shows an example of a regular and irregular polygon:
| Regular pentagon | Irregular pentagon |
|---|---|
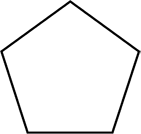 |
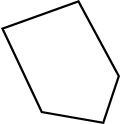 |
| All sides and interior angles are equal | Not all sides and angles are equal |
Convex and concave pentagons
Pentagons can be classified as either convex or concave on top of being classified as regular or irregular.
- Convex pentagon - all interior angles of the pentagon measure < 180°.
- Concave pentagon - at least one interior angle of the pentagon measures > 180°.
The figure below shows an example of a convex and concave pentagon:
| Convex pentagon | Concave pentagon |
|---|---|
 |
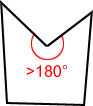 |
| All interior angles < 180° | One or more interior angles > 180° |
Pentagon properties
Below are some properties of all pentagons as well as properties specific to regular pentagons.
Properties of all pentagons
- 5 sides that do not intersect and form a closed shape.
- 5 diagonals.
- 5 vertices.
- 5 internal angles.
- 5 external angles.
- Sum of interior angles is 540°.
- Sum of exterior angles is 360°.
Note that the above does not consider self-intersecting pentagons, which are referred to as pentagrams.
Properties of regular pentagons
A regular pentagon is a pentagon whose sides are equal in length, and whose interior angles are equal in measure; it has the following properties.
- 5 sides with equal measure that do not intersect and form a closed shape.
- 5 diagonals.
- 5 vertices.
- 5 internal angles all measuring 108°.
- 5 external angles all measuring 72°.
All pentagons have interior angles that sum to 540° and exterior angles that sum to 360°.
- Since each of the interior angles in a regular pentagon are equal in measure, each interior angle measures 540°/5 = 108° as shown below.
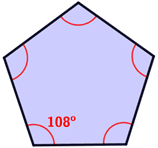
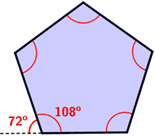
- Each exterior angle of a regular pentagon has an equal measure of 72°.
Diagonals of a pentagon
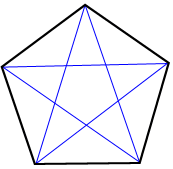
A diagonal is a line segment joining two non-consecutive vertices. Two diagonals can be drawn from each vertex. A total of five diagonals can be drawn for a pentagon. The following figure is an example.
Internal angles of a pentagon
The sum of the interior angles of a pentagon equals 540°.
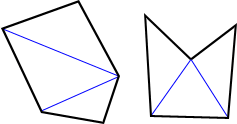
As shown in the figure above, two diagonals can be drawn to divide the hexagon into three triangles. The blue lines above show just one way to divide the pentagon into triangles; there are others. The sum of the interior angles of the three triangles equals the sum of interior angles of the pentagon. Since the sum of the interior angles of a triangle is 180°, the sum of the interior angles of the pentagon is 3 × 180° = 540°.
Symmetry in a regular pentagon
A regular pentagon has 5 lines of symmetry and a rotational symmetry of order 5. This means that it can be rotated in such a way that it will look the same as the original shape 5 times in 360°.
| Lines of symmetry | Rotational symmetry |
|---|---|
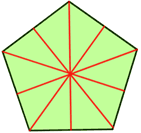 |
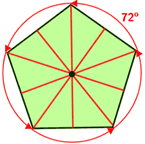 |
| 5 lines of symmetry | Five 72° angles of rotation |
Area of a pentagon
The area of a regular pentagon formula with side length s is:
This formula can be used as long as one side length is known.
Area of a regular pentagon with apothem
The area of a regular pentagon can be calculated using a different formula if the length of a side and apothem are known:
The perimeter of a pentagon is the sum of the length of its sides. For a regular pentagon, the perimeter is p = 5 × s. The apothem of a regular pentagon is the length of the perpendicular line segment formed between the center of the pentagon and one side of the pentagon.
Apothem of a pentagon
The figure below shows the apothem of a pentagon. Note that apothems only exist for regular polygons.

Area of an irregular pentagon
The area of an irregular pentagon can be found by breaking the pentagon up into different polygons, calculating the areas of the respective polygons, then finding the sum of the areas. Depending on the shape of the pentagon, we may be able to break it down into 3 triangles, a rectangle and a triangle, a rectangle and 2 triangles, and so on. However, we would still need to know or be able to find the dimensions of various parts of the pentagon, so this method may not always be possible. Consider the following pentagons.

The above pentagon can be broken down into a rectangle and a triangle, as indicated by the dotted lines. The formula for the area of a rectangle is A = length × width. The area for a triangle is A = ½ × base × height. Note that there are other formulas for the area of a triangle.
The pentagon below can be broken into 3 triangles.

The concave pentagon below can be broken into a rectangle and two triangles.

The above examples show how pentagons can be broken down into various shapes whose areas we can calculate, the sum of which is the area of the pentagon as a whole.
Perimeter of a pentagon
The perimeter of a pentagon is the sum of the sides of the pentagon.
Perimeter of a regular pentagon
The perimeter of a regular pentagon is p = 5 × s, where s is the length of a side of the pentagon. The sides of a regular pentagon all have the same measure, so we only need to know the length of one side to be able to find its perimeter.
Perimeter of an irregular pentagon
To find the perimeter of an irregular pentagon, we must know the lengths of each side of the pentagon. The perimeter is the sum of the lengths of each side. Unlike a regular pentagon, we cannot simply multiply one side by five, since in order for a pentagon to be considered irregular, at least one of the 5 sides must be a different length from the rest. Thus, we must determine how many (if any) of the sides have the same length to find the sum.
