Line of symmetry

A line of symmetry is a line that divides a figure into two identical parts. The figure below shows 3 line of symmetry examples.



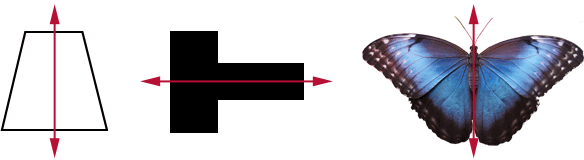
What is a line of symmetry

A line of symmetry is defined as an imaginary line that divides an object into two identical (symmetrical) halves. Another way to think about this is: if a figure can be folded over a line such that each half perfectly overlaps, the line is a line of symmetry.



In the above figure, folding the left half of the square over the red dotted line results in the left half perfectly overlapping with the right half of the square. The dotted red line is therefore a line of symmetry. Specifically, it is a vertical line of symmetry.

Types of lines of symmetry

Generally, there are a few different types of lines of symmetry: vertical, horizontal, and diagonal.

Vertical line of symmetry

A vertical line of symmetry is a vertical line that divides an object into two identical halves. Below is a vertical line of symmetry example:



The figure above shows an isosceles triangle that is divided into two identical halves by a vertical line of symmetry.

Horizontal line of symmetry

A horizontal line of symmetry is a horizontal line that divides an object into two identical halves. Below is a horizontal line of symmetry example:



The square above is divided into two identical halves by a horizontal line of symmetry.

Diagonal line of symmetry

A diagonal line of symmetry is a diagonal line that divides an object into two identical halves. Below is a diagonal line of symmetry example:



The square above is divided into two identical halves by a diagonal line of symmetry.

Number of lines of symmetry

An object can have multiple lines of symmetry. If an object has multiple lines of symmetry, all the lines of symmetry intersect at the center of the object. Consider the following two-dimensional shapes.

No lines of symmetry

A parallelogram has no lines of symmetry because there is no line that can divide it such that the two halves will be mirror images.



Even though the two halves would have the exact same shape, to be a line of symmetry, reflecting one half across the line must cause the half to perfectly overlap the other half. For a paralellogram, we would have to reflect half and then rotate it in order for it to perfectly overlap, so it has no lines of symmetry.

One line of symmetry

An isosceles triangle has one line of symmetry:



Two lines of symmetry

A rectangle has two lines of symmetry: a horizontal and a vertical line of symmetry.



Three lines of symmetry

An equilateral triangle has three lines of symmetry:



Four lines of symmetry

A square has four lines of symmetry:



Infinite lines of symmetry

A circle has infinite lines of symmetry since any line drawn through its center will divide the circle into identical halves.



The figure above just shows a few lines of symmetry. As long as a given line passes through the center of the circle, it is a line of symmetry.

Lines of symmetry in a polygon

A regular polygon always has the same number of lines of symmetry as it does sides.



It is worth noting that all regular polygons are convex. If a polygon is concave, it will not have the same number of lines of symmetry as it does sides. For example, dhe concave decagon shown below only has 5 lines of symmetry. Even though it has ten sides of equal length, it is not a regular polygon because it is a concave shape.



Symmetry in the coordinate plane

In the coordinate plane, the graph of an equation can have symmetry about the x-, y-axis, or some other line.

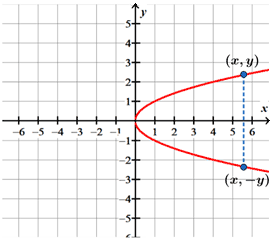
x-axis symmetry

A graph is said to have x-axis symmetry if whenever the point, (x, y), is on the graph, then (x, -y) is also on the graph.



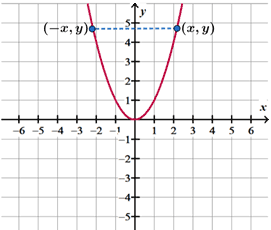
y-axis symmetry

A graph has y-axis symmetry if whenever the point (x, y) is on the graph, then (-x, y) is also on the graph.



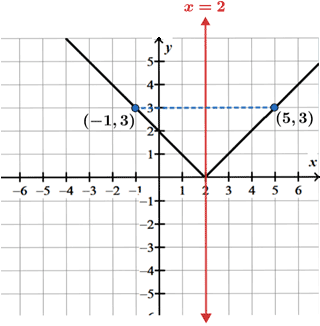
Symmetry about a line

It is also possible for the graph to have symmetry about some other line.



Line of symmetry equation

Given a quadratic equation in standard form, ax2 + bx + c, we can find the equation of the line of symmetry of the parabola as:



For example, given the equation 2x2 + 3x - 5, the equation for the axis of symmetry of the parabola is:



Thus, the parabola has a vertical line of symmetry at .


Mathematics of symmetry

Mathematically, a line of symmetry is a line of reflection that maps any point on the figure back to the figure.

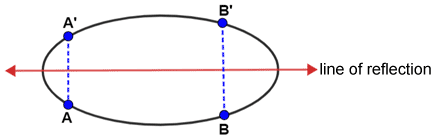
The line that cuts through the major axis of the ellipse above is a line of symmetry. When A and B are reflected across it, they are mapped to A' and B', also on the ellipse. This is true for any point on the ellipse.

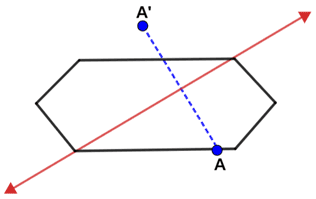
Not all lines of reflection are also lines of symmetry just because they divide the figure into two equal parts. Although the line through the vertices of the irregular hexagon below divides it into two equal parts, it is not a line of symmetry. Point A on the hexagon reflects to A' which is not on the hexagon.

A line of symmetry is known as a rigid motion (or transformation) in geometry since the figure that is reflected across it does not change size or shape and is only "flipped" across the line of symmetry.

Symmetric and asymmetric