Surface area of a sphere
The surface area of a sphere can be thought of as the amount of material, such as wrapping paper, that it would take to exactly cover its entire surface.
We see surface area all the time in our everyday lives. If we were to pop a basketball, or peel an orange, then lay them flat and measure the total area covered, the result would be their surface areas.
Surface area formula
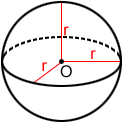
The surface area, S, of a sphere with radius r is:
S = 4πr2
Example:
The volume of a sphere is 972π. What is the sphere's surface area?
First find r:
729 = r3
r = 9
Now that we know r, we can plug it into the surface area formula:
S = 4πr2 = 4π × 92 = 324π
Surface area of a hemisphere
A hemisphere is created by a plane intersecting a sphere's center.
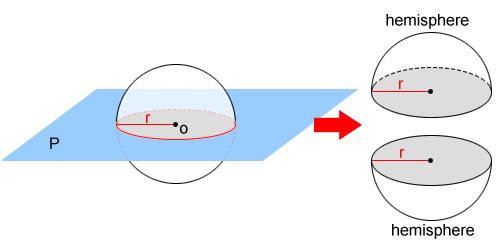
In the figure above, plane P intersects sphere O through its center, creating two hemispheres of equal size. Since a hemisphere is half of a sphere, they share many of the same properties. The surface area of a sphere is 4πr2. Since a hemisphere is half of a sphere, its surface area, S, is half the surface area of a sphere plus the area of the circular base (shown in gray) created by intersection of the plane and sphere:
S = 4πr2/2 + πr2 = 3πr2
where r is the radius of the hemisphere.
Did you know?
Changing the volume and surface area of a soccer ball also changes the way it reacts when kicked, headed, or thrown. As more air is pumped into the ball, the volume increases, making the ball harder, which generally increases the distance it can be kicked. The surface area also increases, making it easier to head or throw. A properly pumped soccer ball usually makes for a better soccer match.
