Surface area
In geometry, the surface area of a 3D shape or geometric figure is the amount of space occupied by its surfaces.
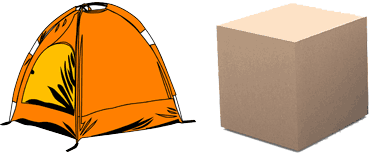
In the figures above, the amount of material it takes to make the tent to the left is the tent's surface area. The amount of cardboard used to make the box to the right is its surface area.
Surface area is often measured in square units, such as square meters and square feet.
Finding surface area
One common way to find the surface area of a 3D shape is to unfold the shape or figure into a flat (2D) figure, referred to as a net. The dimensions of each surface can then be measured in order to find their areas. The sum of the areas of all the surfaces in a shape is its surface area. This method works well for polyhedrons, but is not as effective for shapes with curved surfaces.
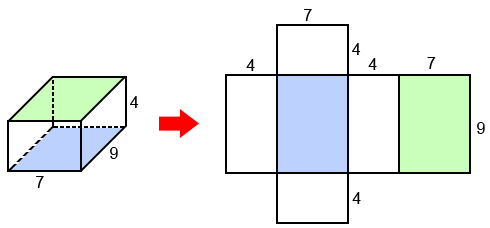
The rectangular prism above is unfolded to create a 2D shape made up of the surfaces of the prism. To find the surface area, S, of the rectangular prism, find the sum of the areas of each rectangle in the figure.
There are two rectangles with lengths of 7 and widths of 4, two rectangles with lengths of 9 and widths of 4, and two rectangles with lengths of 9 and widths of 7, so the surface area of the prism is:
S = 2(7 × 4) + 2(9 × 4) + 2(9 × 7) = 254
Surface area formulas
Many common objects have well-defined formulas for finding their surface areas.
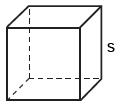
Cube
The surface area, S, of a cube with edge, s, is:
S = 6s2
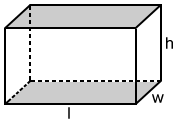
Rectangular prism
The surface area, S, of a rectangular prism is:
S = 2lw + 2lh + 2wh
where l is the length, w is the width, and h is the height of the rectangular prism.
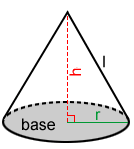
Right cone
The surface area, S, of a right cone is:
S = πr2 + πrl
where r is the radius of the base and l is the slant height.
If the height of the cone is given, the surface area is:
where h is the height of the right cone.
In both these formulas, πr2 is the area of the base and πrl or is the area of its lateral surface.
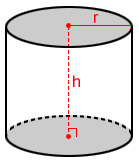
Right cylinder
The surface area, S, of a right cylinder is:
S = 2πr2 + 2πrh
where r is the radius of the base and h is the height.
2πr2 is the area of the two bases and 2πrh is the area its lateral surface.
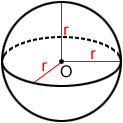
Sphere
The surface area, S, of sphere with radius, r, is:
S = 4πr2
Example:
Approximate the height of a right cylinder that has a surface area of 752 and a base with a radius of 4.
Substituting S = 752 and r = 4 into the formula for the surface area of a right cylinder:
752 = 2π(4)2 + 2π(4)h
752 = 32π + 8πh
752 - 32π = 8πh
Surface area of a composite figure
3D composite figures are figures that are made up of two or more types of figures. Their surface areas can be calculated by breaking them down into their components, calculating the surface area of each component, then summing the surface areas.
Example:
Find the surface area of the perfect ice-cream cone composed of a right cone and a hemisphere.
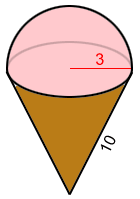
Let S be the surface area of the composite figure. The slant height of the right cone is 10 and its base radius is 3. The hemisphere also has a radius of 3. Let S1 be the surface area of the right cone's lateral surface and S2 be the surface area of the hemisphere:
S1 = πrl = π×3×10 = 30π
S = S1 + S2 = 30π + 18π = 48π
