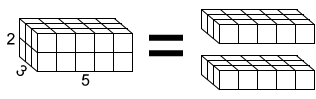Volume formula
The volume of a 3D shape or geometric figure is the amount of space it contains. Volume is well-defined for many common shapes; the formulas for some common shapes are shown below.
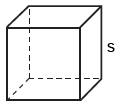
Cube
The volume, V, of a cube with edge, s, is:
V = s3
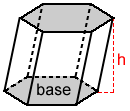
Prism
The volume, V, of a prism is:
V = Bh
where B is area of the base and h is the height of the prism.
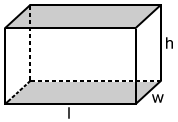
Rectangular prism
The volume, V, of a rectangular prism is:
V = lwh
where l is the length, w is the width, and h is the height of the rectangular prism.
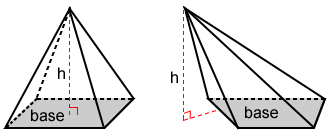
Pyramid
The volume, V, of a pyramid is:
where B is area of the base and h is the height of the pyramid.
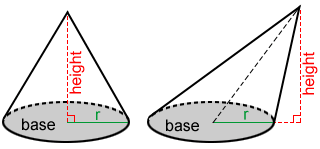
Cone
The volume, V, of a cone is:
where r is radius of the base and h is the height of the cone.
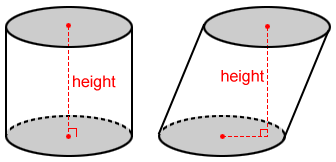
Cylinder
The volume, V, of a cylinder is:
V = πr2 h
where r is the radius of the base and h is the height of the cylinder.
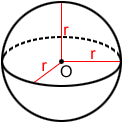
Sphere
The volume, V, of a sphere with radius, r, is:
Example:
Find the volume of the rectangular prism below.
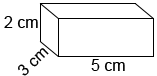
The volume of the rectangular prism is:
V = 5 × 3 × 2 = 30 cm3
Volume of a composite figure
3D composite figures are figures that are made up of two or more types of figures. Their volumes can be calculated by breaking them down into their components, calculating the volumes of each component, then summing them to find the total volume of the composite figure.
Example:
The grain silo below is made up of a right cylinder and a right circular cone. Find the amount of grain, in cubic meters, the silo can hold when full.
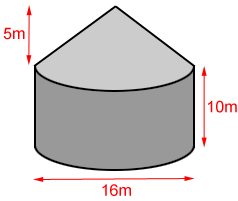
The cylinder has a radius of 8 m and height of 10 m. The cone also has a radius of 8 m, since it sits on top of the cylinder, and its height is 5 m.
The volume of the cylinder is:
Vcylinder = π × 82 × 10 = 640π m3
The volume of the cone is:
The volume, V, of the silo is the sum of the volumes of the cylinder and cone:
The silo can hold 2345.72 cubic meters of grain.
Using a unit cube to find volume
One way to find the volume of a figure is to determine how many unit cubes it takes to fill the figure. A unit cube has side lengths of 1 and a volume of 1.
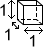
The rectangular prism below has a length of 5, width of 3, and height of 2.
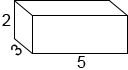
You can evenly stack 2 layers of unit cubes, containing a total of 15 unit cubes each into the rectangular prism to find its volume of 30 unit cubes.