Volume of a cube
The volume of a cube is the amount of space it encloses. The cubic packing box below is an example of a common everyday object that can help illustrate the concept of volume. If we were able to pack the box perfectly, such that there was no space in the box that wasn't filled, and we could tape it closed perfectly, the volume of the box is the amount of stuff we packed in.

Formula for the volume of a cube
The volume, V, of a cube is:
V = s3
where s is a side length of the cube.
The volume of a cube can be found by determining how many unit cubes it takes to fill the cube. A unit cube is a cube with side lengths of 1 and a volume of 1.
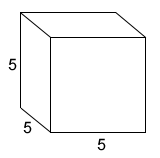
The cube below has side lengths of 5.
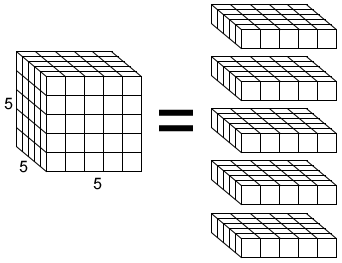
You can evenly stack 5 layers of unit cubes containing a total of 25 unit cubes each into the cube, as shown below, to find that it has a volume of 125 unit cubes.
This method works for cubes of any size, hence why the formula for the volume of a cube is:
V = s3
Finding the volume of a cube using its diagonal
We can find the volume of a cube given the length of its diagonal using the formula
where d is the length of the diagonal.
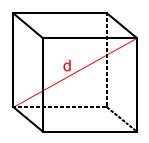
A diagonal of a cube is a line segment whose endpoints are two opposite verticies of the cube. All the diagonals of a cube have equal length, so any diagonal can be used for the formula.
To write the diagonal in terms of side s, we need to first find the length of a diagonal for one of the cube's faces.
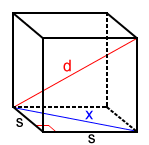
Diagonal x for the bottom face of the cube above can be found using the Pythagorean theorem, since a right triangle is formed by x and two adjacent sides of the face.
x2 = s2 + s2
We can use the Pythagorean theorem again to find diagonal of the cube, since the cube's diagonal, the diagonal of one of its faces, and a side of the cube form another right triangle, as shown below.
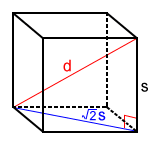
Solving for s:
Substituting the value for s written in terms of d into the volume formula for a cube:
