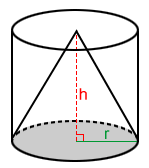
Volume of a cone
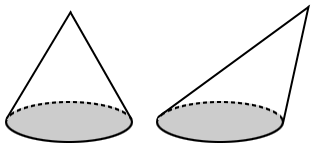
The volume of a cone is the amount of space enclosed by the cone. Below are two types of cones. The one on the left is a right cone, and the one on the right is an oblique cone.
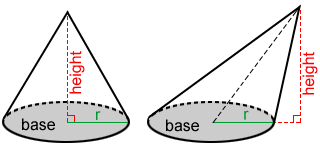
Formula for the volume of a cone
The formula for the volume, V, of a cone is:
where r is the radius of the base and h is the height of the cone.
If the base area, B, of the cone is given, the volume is:
Using slant height to find the volume of a cone
The slant height of a right cone can be used to find its volume.
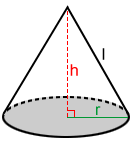
The slant height, l, shown above for the right cone, is the length of a line segment drawn from the vertex (apex) of the cone to a point on the base's circumference.
A right triangle can be formed between the height, radius, and slant height, so we can use the Pythagorean theorem to find the following relationships:
| r2 + h2 = l2 |
In terms of l and h, the volume of a right cone is,
In terms of l and r, the volume of a right cone is,
Example:
Approximate the radius of a right cone that has a volume of 64π and a slant height that is twice the length of the cone's height.
First, find h by substituting V = 64π and l = 2h into the volume formula.
| 64 = h3 |
| h = 4 |
Since l = 2h, l = 2×4 = 8. Substitute l and h into to find r.
A cylinder and inscribed cone
The formula for the volume of a cylinder is πr2h. The volume of a cone that has the same base and height is exactly one-third the volume of the cylinder. This is true for any cone that can be inscribed in a cylinder as long as the base and height are the same.