Surface area of a cylinder
In geometry, the surface area of a cylinder is the amount of space occupied by its surfaces. The surface area of a cylinder is made up of its two bases (grey) and its lateral surface (white), as shown in the figure below.
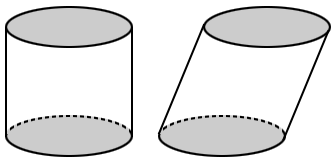
Cylinders are often categorized as right cylinders and oblique cylinders. If the line segment joining the centers of the two bases is perpendicular to both bases, it is a right cylinder. If not, it is an oblique cylinder. In the figure above, the cylinder on the left is a right cylinder and the cylinder on the right is an oblique cylinder.
Surface area of a right cylinder
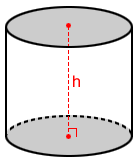
The surface area, S, of a right cylinder that has a height of h and a base with radius r is
S = 2πr2 + 2πrh
where 2πr2 is the area of the two bases and 2πrh is the area of the lateral surface.
One way to visualize how this formula works is to form a net. A net, in the context of geometry, is a pattern that can be folded to form a 3D geometric figure. When it is unfolded, it allows us to see each of the components of the 3D figure in 2D. The sum of the areas of each figure in the net is the surface area of the figure that the net forms, in this case a right cylinder:
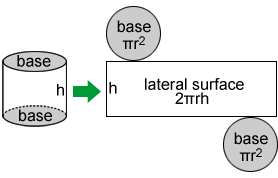
The surface area of the right cylinder is the sum of the areas of the 2 circles and the rectangle.
S = πr2 + πr2 + 2πrh
S = 2πr2 + 2πrh
Surface area of a tube
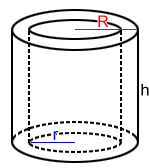
A tube is a hollow cylinder. If we were to remove a cylinder with a smaller radius from a larger cylinder, the remaining figure is a tube. The surface area of a tube is:
S = 2πR2 - 2πr2 + 2πRh + 2πrh
where R is the outer radius, r is the inner radius, and h is the length of the tube. 2πR2 - 2πr2 is the area of the base, 2πRh is the area of the outer lateral surface, and 2πrh is the area of the inner lateral surface.
Example:
What is the surface area of the tube shown below?
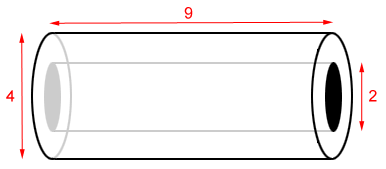
The outer radius of the tube is 4 ÷ 2 = 2 and the inner radius is 2 ÷ 2 = 1.
| S = | 2πR2 - 2πr2 + 2πRh + 2πrh |
| = | 2π(2)2 - 2π(1)2 + 2π×2×9 + 2π×1×9 |
| = | 8π - 2π + 36π + 18π |
| = | 60π |
