Volume of a cylinder
The volume of a cylinder is the amount of space it encloses. Below is a paint bucket in the shape of cylinder. The volume of the cylinder is the maximum amount of paint the bucket can hold.

Formula for the volume of a cylinder
The formula for the volume, V, of a cylinder is:
V = π r2 h
where r is radius of the base and h is the height of the cylinder.
If the base area, B, of the cylinder is given, the volume is:
V = Bh
Example:
The base radius of a cylinder is 2 and the height of the cylinder is 3. What is the volume of the cylinder?
V = π × 22 × 3 = 12π
Volume of a tube
A tube is a hollow cylinder, like the one shown below. The volume of a tube is:
V = πh(R2 - r2)
where R is the outer radius, r is the inner radius, and h is the length of the tube.
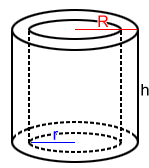
The volume of a tube can be used to determine how much material is needed to construct shapes such as a hose or a pipe.
Example:
A cement drainage pipe has a length of 96 inches, outer diameter of 28 inches, and inner diameter of 24 inches. What is the volume of the pipe (how much cement do we need to build the pipe)?
The radius of the outer cylinder is R = 14 and the inner radius is r = 12. The height of both cylinders is 96 so the volume of the pipe is
V = π × 96 × (142 - 122) = 4992π ≈ 15,682.83
Therefore, the cement needed to build the pipe is 15,682.83 cubic inches
Volume of a substance in a partially filled cylinder
Volume in an upright cylinder
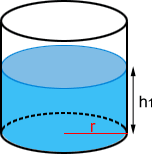
When the cylinder is upright, or resting on one of its bases, we can find the volume of a substance in the cylinder as long as we know the height the substance reaches in the cylinder. The formula is the same as that for the volume of a right cylinder:
V = π r2 h1
where r is radius of the base and h1 is the height the substance reaches in the cylinder.
Example:
A water tank in the shape of a cylinder has a radius of 5 and a height of 9. If the tank is two-thirds full, how much water does it contain?
Since the tank is two-thirds full, the height, h1, of the water level in the tank is 2/3 of the height of the tank:
h1 = 2/3 × 9 = 6
Plugging this into the volume formula:
V = π × 52 × 6 = 150π
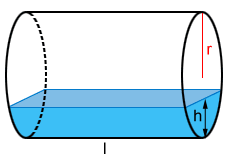
Volume in a cylinder resting on its side
The volume of a substance in a cylinder resting on its lateral surface can be found using the following formula:
where r is the radius of the base of the cylinder, h is the height that the substance reaches in the cylinder, and l is the length between the bases of the cylinder.