Law of Cosines
In trigonometry, the Law of Cosines relates the sides and angles of triangles. Given the triangle below, where A, B, and C are the angle measures of the triangle, and a, b, and c are its sides, the Law of Cosines states:
a2 = b2 + c2 - 2bc·cos(A)
b2 = a2 + c2 - 2ac·cos(B)
c2 = a2 + b2 - 2ab·cos(C)
The right triangle definition of cosine () can only be used with right triangles. It cannot be used to relate the sides and angles of oblique (non-right) triangles. However, there are many other relationships we can use when working with oblique triangles. The Law of Cosines is one such relationship. Another is the Law of Sines.
The Law of Cosines can also be rearranged to provide equations for finding angles A, B, and C. Using the equation that includes cos(A):
a2 = b2 + c2 - 2bc·cos(A)
We can solve the equations involving cos(B) and cos(C) similarly to yield:
When to use the Law of Cosines
The Law of Cosines can be used to solve for the sides and angles of an oblique triangle when the following measurements are known:
- Three sides: SSS (side-side-side)
- Two sides and an included angle: SAS (side-angle-side)
Example:
For triangle ABC, A = 60°, b = 4, and c = 7. Find a:
We know two sides and their included angle (angle between the two sides) so we can use the Law of Cosines as follows:
a2 = b2 + c2 - 2bc·cos(A)
a2 = 42 + 72 - 2·4·7·cos(60°)
a2 = 37
Example:
Find the measures for the angles in triangle ABC if a = 7, b = 13, and c = 18:
Since we know all the sides, we can use the equations derived from the Law of Cosines to find the angles. Starting with the largest side:
C = cos-1(-0.5824) ≈ 125.62°
We can find A or B using the Law of Cosines or the Law of Sines. Using the Law of Cosines to find A:
A = cos-1(0.9487) ≈ 18.43°
We can find B using the fact that the sum of the angles of a triangle is equal to 180°:
B = 180° - (18.43° + 125.62°) = 35.95°
Proof of the Law of Cosines
To show how the Law of Cosines works using the relationship c2 = a2 + b2 - 2ab·cos(C) (the other two relationships can be proven similarly), draw an altitude h from angle B to side b, as shown below.
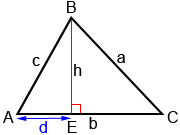
Altitude h divides triangle ABC into right triangles AEB and CEB. We can then use the right-triangle definitions of sine () and cosine (
), as well as the Pythagorean theorem to determine measures for triangles AEB and CEB.
Triangle AEB:
c2 = h2 + d2
Triangle CEB:
sin(C) = and h = a·sin(C)
cos(C) = and d = b - a·cos(C)
Substituting these values of h and d into the equation c2 = h2 + d2:
c2 = (a·sin(C))2 + (b - a·cos(C))2
c2 = a2·sin2(C) + b2 - 2ab·cos(C) + a2·cos2(C)
c2 = a2·(sin2(C) + cos2(C)) + b2 - 2ab·cos(C)
sin2(C) + cos2(C) = 1 is a trigonometric identity. Substituting 1 in for sin2(C) + cos2(C):
c2 = a2 × 1 + b2 - 2ab·cos(C)
c2 = a2 + b2 - 2ab·cos(C)
If C = 90°,
c2 = a2 + b2 - 2ab·cos(90°)
c2 = a2 + b2 - 2ab × 0
c2 = a2 + b2
yielding the Pythagorean theorem.
