Unit Circle
A unit circle is a circle with a radius of 1.
What is the unit circle
In trigonometry, the unit circle is a circle with of radius 1 that is centered at the origin of the Cartesian coordinate plane. The unit circle helps us generalize trigonometric functions, making it easier for us to work with them since it lets us find sine and cosine values given a point on the unit circle. We can then use sine and cosine to find values for other trigonometric functions through use of their relationships along with trigonometric identities.
Unit circle equation
The equation of a unit circle can be found using the Pythagorean theorem a2 + b2 = c2. Consider the following figure:
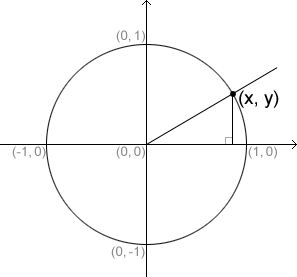
When a ray is drawn from the origin of the unit circle, it will intersect the unit circle at a point (x, y) and form a right triangle with the x-axis, as shown above. The hypotenuse of the right triangle is equal to the radius of the unit circle, so it will always be 1. Based on the Pythagorean Theorem, the equation of the unit circle is therefore:
x2 + y2 = 1
This is true for all points on the unit circle, not just those in the first quadrant, and is useful for defining the trigonometric functions in terms of the unit circle.
Unit circle: sine, cosine, tangent
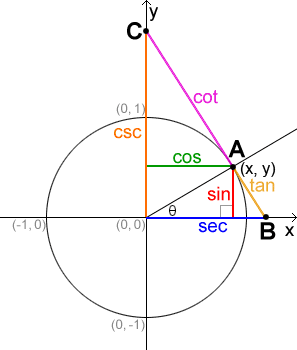
The unit circle provides a simple way to define trigonometric functions. This is because of the relationships between the functions, the unit circle, and their right triangle definitions. For reference, the right triangle definitions of sine and cosine are listed below:
Then, since we know that the hypotenuse of the unit circle is its radius, which is always equal to 1, we know that sine is equal to the opposite side of the triangle, which corresponds to the y-value of the unit circle at the given angle. Similarly, cosine is equal to the adjacent side of the triangle, which corresponds to the x-value of the unit circle at the given angle. Algebraically:
From this relationship, we can derive the rest of the trigonometric relationships, as shown in the table below.
| Unit circle definition of trigonometric functions | |
|---|---|
The figure below shows the geometric representations of the trigonometric functions in the unit circle.
How to use the unit circle
Using the unit circle definitions, we can evaluate any of the trigonometric functions by finding the x and y-values corresponding to the given angles. However, there are only a few angles for which we can exactly evaluate trigonometric functions without a calculator. These are referred to as special angles.
Special angles
The special trigonometric angles are 30°, 45° and, 60°. In radians, they correspond to respectively. These are the angles that we can evaluate exactly using right triangle trigonometric relationships. Below is a table of the values of these angles, as well as a figure of the values on a unit circle.
| Angle | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 1 | |||
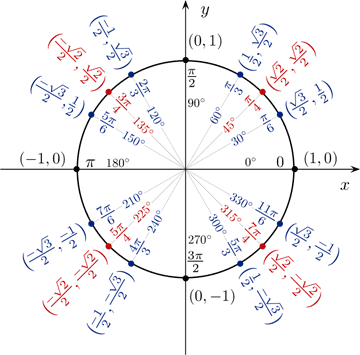
As can be seen from the table or the unit circle above, there are three values to remember: . Because of the nature of the unit circle, these values are the same for their respective angles in different quadrants on the unit circle, with the only difference being their signs based on the quadrant the angle is in. Therefore, remembering these three values as well as the reference angles (described below) 30°, 45° and 60° will enable you to fill in all the values on the unit circle.
The other angles on the unit circle to remember are those whose terminal sides lie on the x- or y-axis: 0° or 0 (which has equivalent sine and cosine values as 360° or 2π), 90° or , 180° or π and, 270° or
. At any of these angles, sin(θ) or cos(θ) has a value of –1, 0, or 1:
| Angle | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 0 | 1 | 0 | |
| 1 | 0 | Undefined | |
| 180° or π | 0 | -1 | 0 |
| -1 | 0 | Undefined |
Reference angles
Recall that a reference angle is the smallest positive acute angle formed by the terminal side of the angle and the horizontal axis. Reference angles enable us to relate the values of each special angle in each quadrant. For example, given that the reference angle is 30°, the corresponding angles (that share the same cosine and sine values) in each quadrant are 150°, 210°, and 330°. All these angles share the same values of sine and cosine as 30°, but have different signs. The formulas for determining the reference angle in each quadrant are as follows:
- Reference angle = given angle
- Reference angle = 180° - given angle
- Reference angle = given angle - 180°
- Reference angle = 360° - given angle
Using the same 30° example, in the first quadrant, the reference angle is 30°. In the second quadrant, given an angle of 150°, the reference angle is 180° - 150° = 30°, and so on. By determining the reference angle, we can find the cosine and sine values for the reference angle, which are the same as the values for the given angle, except that we must account for sign.
How to memorize the unit circle
One method that may help with memorizing the common trigonometric values is to express all the values of sin(θ) as fractions involving a square root. Starting from 0° and progressing through 90°, sin(0°) = 0 = . The subsequent values, sin(30°), sin(45°), sin(60°), and sin(90°) follow a pattern such that, using the value of sin(0°) as a reference, to find the values of sine for the subsequent angles, we simply increase the number under the radical sign in the numerator by 1, as shown below.
| θ | 0° | 30° | 45° | 60° | 90° |
| sin(θ) |
The values of sine from 0° through -90° follows the same pattern except that the values are negative instead of positive since sine is negative in quadrant IV. This pattern repeats periodically for the respective angle measurements, and we can identify the values of sin(θ) based on the position of θ in the unit circle, taking the sign of sine into consideration: sine is positive in quadrants I and II and negative in quadrants III and IV.
A similar memorization method can be used for cosine. Starting from 0° and progressing through 90°, cos(0°)=1=. The subsequent values, cos(30°), cos(45°), cos(60°), and cos(90°) follow a pattern such that, using the value of cos(0°) as a reference, to find the values of cosine for the subsequent angles, we simply decrease the number under the radical sign in the numerator by 1, as shown below:
| θ | 0° | 30° | 45° | 60° | 90° |
| cos(θ) |
From 90° to 180°, we increase the number under the radical by 1 instead, but also must take into account the quadrant that the angle is in. Cosine is negative in quadrants II and III, so the values will be equal but negative. In quadrants I and IV, the values will be positive. This pattern repeats periodically for the respective angle measurements.
As long as we remember these values, it is possible to determine all of the trigonometric values for the special angles in each quadrant using reference angles.
