Angle

An angle is formed by rotating a ray around its endpoint. The initial side of an angle is the beginning position of the ray and the terminal side is the position of the ray after it is rotated. The endpoint that the ray is rotated around to form the angle is called the vertex.

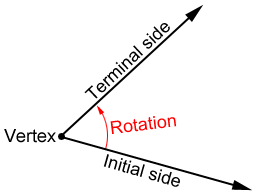
The measure of an angle is the amount of turn or rotation from its initial side to the terminal side. The amount of the turn is typically measured in degrees (°).

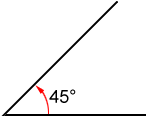
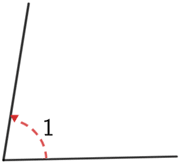
Angles can also be formed by rotating a line segment around one of its endpoints. Below is an angle formed by rotating a line segment around its left endpoint 45° counterclockwise as noted by the circular arc in red.

While we can create an angle by rotating a line or line segment around an endpoint, most of the angles we will look at are already formed by two rays or line segments that share a common endpoint.

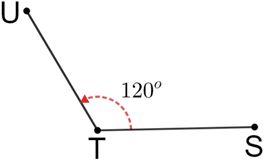
Here's another angle, formed by line segments TU and TS, that has a measure of 120°.

There are different ways to measure angles. One way to measure an angle is with a tool called a protractor. Click here to see how to use a protractor to measure an angle or draw an angle with a certain measurement.

Name angles

We can name an angle by the endpoints of the line segments that form it. So, the angle above can be named as ∠STU or ∠UTS, where ∠ is the angle symbol. Notice the vertex at T for the angle is placed in the middle when the angle is named by the endpoints.

Angles can also be named using lower case letters, Greek letters, or even numbers.

By the angle's vertex: ∠b

By the Greek letter θ: ∠θ

By the endpoints of the line segments:
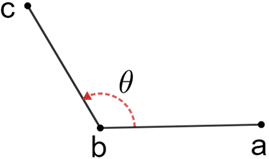
∠abc or ∠cba

By the number: ∠1

Be careful when naming angles that share a common vertex. There are 3 angles in the diagram below.

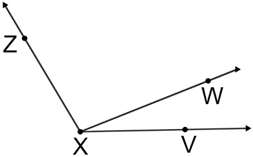
∠ZXY, ∠WXV, or ∠ZXV

Be careful not to name any of the 3 angles as only ∠X since X is the vertex to all 3 of the angles. Angles ∠VXW and ∠ZXW are called adjacent angles because they share a common side or ray and vertex but have no common points in their interiors.

Classify angles

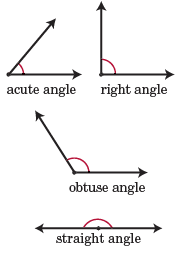
In typical Geometry courses, angles have a measure greater than or equal to 0° and less than or equal to 180°. The measure of an angle also determines what it is called. Below are the names of angles based on their measure, as well as figures of what they look like:

Acute angle - 0° to 90°
Right angle - 90°
Obtuse angle - 90° to 180°
Straight angle - 180°

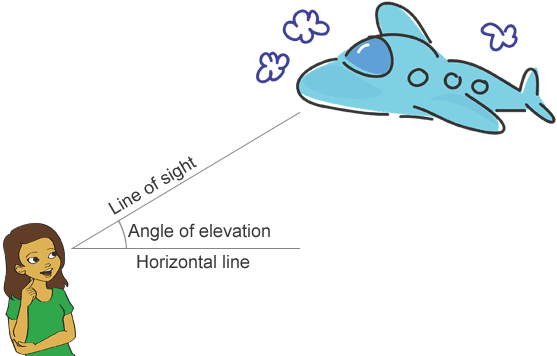
Angles in everyday life

Angles are everywhere. Whenever you look up to the sky to spot a plane flying overhead, you create an angle of elevation between a horizontal line at your eye level with the line of sight to the plane. Engineers use angles to build freeways and bridges, carpenters use angles to build structures such as houses. The lines of longitude and latitude around the earth are formed by angles as well.