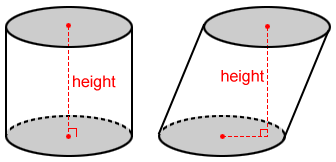
Cylinder

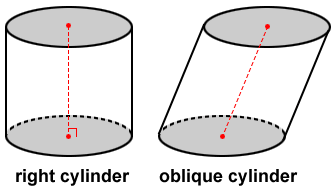
A cylinder is a 3D geometric figure with two identical parallel bases (usually circles) and a curved surface that "wraps" around the bases. In the figure below are two types of cylinders.

Below are some real-life examples of cylinders. On the left is an image of a cylindrical pipe organ. On the top right is a cylindrical tanker truck, and on the bottom right are some industrial cylindrical tanks.

Properties of a cylinder

A cylinder is made up of two congruent, parallel bases, that are usually circles, and a curved lateral surface that meets the bases at their perimeters (circumferences for circular cylinders).

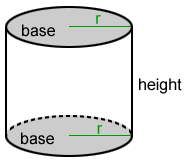
The height, h, of a cylinder is the length of a line segment perpendicular to the bases. The radius of a circular cylinder is equal to that of its bases, as shown above.

Any cross section that is parallel to the bases of a cylinder forms a shape that is congruent to both bases.

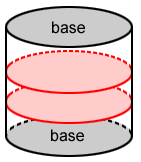
Two circular cross sections for the circular cylinder are shown in red above. They are congruent to both bases. This is true for any parallel cross section of a cylinder.

Classifying cylinders

The line segment connecting the centers of the bases can be used to determine whether the cylinder is a right cylinder or an oblique cylinder. The line segment joining the centers of the two bases of a right cylinder is perpendicular to both bases. If not, it is an oblique cylinder. An oblique cylinder appears to be leaning.

Surface area of a right circular cylinder

The surface area, A, of a right circular cylinder is

A = 2πr² + 2πrh

Where r is the radius of the base and h is the height. On the right side of the equation, 2πr² is the area of the two bases and 2πrh is the area of the lateral surface.

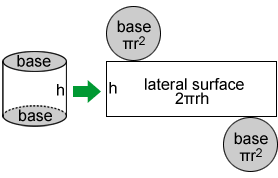
If you cut along the height of a right circular cylinder and lay it out flat, you get a 2D net, as shown above. The area of one circular base is πr². The height of the rectangular lateral surface is h. The length is the same as the circumference of the bases, or 2πr. Therefore, the area of the lateral surface is 2πrh.

Volume of a cylinder

The volume, V, of a cylinder is the area of one of its bases (B) times its height (h).

V = Bh

For a circular cylinder with base radius, r, the base area is πr². Therefore, the volume of a circular cylinder is

V = πr²h