0D

In geometry, the term zero dimensions, or 0D, refers to the property of having no dimensions (length, height, width, depth, etc.). A point is an example of a geometric object that has zero dimensions, and is typically represented using a dot or small circle:

·

A point having zero dimensions means that it can only be described in terms of its position in space; to say "a point has a diameter of 1 cm" wouldn't make sense, even though a point on a page does have some dimension.

A point in a coordinate plane is most commonly indicated using a dot and a set of coordinates that describe its position. Below are examples of a point in a 2D coordinate plane (left) and a 3D coordinate space (right). The coordinates in each are referred to as an ordered pair (2D) and an ordered triple (3D), and describe the position of the point relative to the origin.

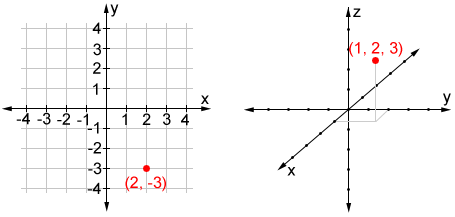
The points in the figures above are located at (2, -3) and (1, 2, 3). These describe the position of the points within the coordinate system, but the points have no dimensions.

Other dimensions

In geometry, we usually consider 0-dimensional, 1-dimensional, 2-dimensional, and 3-dimensional space.

1D

A one-dimensional object only has 1 dimension. Usually, this dimension is length. A line, ray, or line segment, are all examples of 1D objects. Only one coordinate (3) is necessary to specify the position of point A on the number line below.

2D

A square is a 2D object; it has length and width. To specify the point A on the square, we need 2 coordinates, not just 1 as we would on a line. The dotted lines represent the 2 dimensions of the square, which shows that 2 coordinates are necessary to specify the position of point A within the square.

3D

A cube is a 3D object; it has length, width, and height. The dotted lines represent the 3 dimensions of the cube, which shows that 3 coordinates are necessary to specify the position of point A within the cube.