home / geometry / coordinate plane / plotting a point

Plotting a point

Plotting a point in a coordinate system refers to marking a point in a coordinate plane given its coordinates.

Plotting a point on a 2D coordinate plane

A 2D coordinate plane is formed by the intersection of a horizontal number line called the x-axis and a vertical number line called the y-axis. The two axes (plural for axis) intersect at a point called the origin of the coordinate plane and form four right angles. A grid is often drawn on a coordinate plane to make it easier to plot points.

The position of a point in a 2D coordinate plane is written as an ordered pair of numbers (x, y). The first number in the pair corresponds to the position of the point in the horizontal direction (x-axis) and the second number corresponds to its vertical position (y-axis).

An ordered pair describes the position of a point in the coordinate plane relative to the origin. To plot a point (x, y) in the coordinate plane, count x squares along the x-axis from the origin then count y squares in the direction of the the y-axis.

Example:

Plot points A (4, 3), B (-3, 0), and C (3, -2) on a coordinate plane.

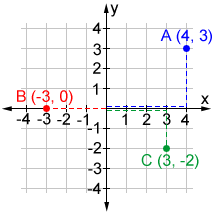
Starting from the origin, follow the steps below to plot the points.

To plot point A, starting from the origin, move right 4 units along the x-axis, then move up 3 units in the direction of the y-axis. Draw a point and label it "A."
For point B, move left 3 units along the x-axis. Since the y-coordinate is 0, there is no vertical component. Draw a point and label it "B."
For point C, move right 3 units along the x-axis then move down 2 units in the direction of the y-axis. Draw a point and label it "C."

Did you know?

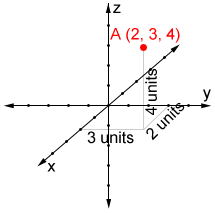
There are many other coordinate systems used today. Above, we only talked about points in 2D, but there are also 3D coordinate systems used for graphing points, equations, and figures in 3D space. A 3D coordinate system contains three axes; the x-axis, y-axis, and the z-axis. A point in the 3D coordinate system is an ordered triple (x, y, z). Below is an example of a point plotted in a 3D coordinate system.