Equidistant
Two or more figures that are equal in distance from each other, or equal in distance from a given point, are said to be equidistant, as in the figure below.

We see things that are equidistant all around us. In the diagram below, the rails on a railroad track are equidistant, and each passenger car on the Ferris wheel is equidistant from the Ferris wheel's center.

The midpoint formula and the distance formula can be used to find a point that is equidistant from two points and to determine whether two or more figures are equidistant.
Midpoint: If (x1, y1) and (x2, y2) are the endpoints of a line segment in a 2D coordinate plane, the midpoint of the line segment is
The midpoint, by definition, is equidistant from each end of the line segment.
Distance formula: If (x1, y1) and (x2, y2) are two points in a coordinate plane, the distance, d, between the two points is
Example:
Find the midpoint of line segment AB given that the coordinates of points A and B are (1, -2) and (5, 6) respectively. Verify the midpoint by finding its distance from points A and B.
i. Midpoint:
ii. Distance between A and the midpoint:
| d1 = | |
| = | |
| = |
iii. Distance between B and the midpoint:
| d2 = | |
| = | |
| = |
Both points A and B are from the midpoint which confirms that the midpoint is equidistant to points A and B.
Equidistance in geometry
The concept of equidistance is used throughout geometry. Below are just a few examples.
Parallel lines
Parallel lines are equidistant from each other; any point on one line is always equal in distance from the other line.

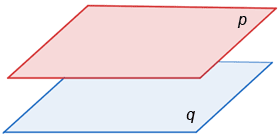
Parallel planes
Like parallel lines, parallel planes are also equidistant from each other. Any point on one plane is equal in distance from the other plane.
Perpendicular bisectors
Any point on the perpendicular bisector of a line segment is equidistant from the segment's endpoints.
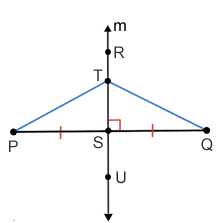
Line m is the perpendicular bisector of line segment PQ, shown above. Points R, T, S, and U on line m are all equidistant from P and Q.
Circles
Each point that lies on a circle is equidistant from the center of the circle. A radius is a line segment that has endpoints on both the circle's center and the circle itself. All radii (plural for radius) have an equal length.
Triangles
The circumcenter of a triangle is the point of intersection of the three perpendicular bisectors of the triangle's sides. The circumcenter is equidistant from each of the triangle's vertices (plural for vertex).
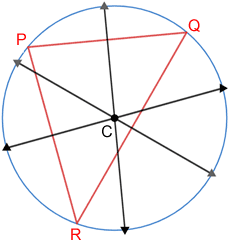
The circumcenter of triangle PQR above is point C. Point C is equidistant from vertices P, Q, and R. Since C is equidistant from P, Q, and R, it is possible to draw a circle centered at C that intersects all the vertices of the triangle. This circle is called the circumcircle of the triangle.
Angle bisectors
Any point on an angle's bisector is equidistant from its sides.
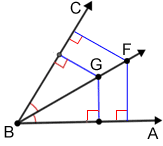
Ray BG bisects angle ABC above. Points G and F are equidistant from sides BA and BC. The distance from each point on the angle bisector is the length of the line segment perpendicular to each side, as shown by the blue line segments.
Parabolas
A parabola is the set of all points that is equidistant from a fixed point, called the focus, and a fixed line called the directrix.
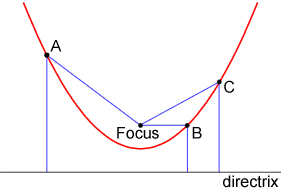
Points A, B, and C, as well as any point on the parabola, are all equidistant from the parabola's focus point and directrix.
