Coordinate plane
A coordinate plane is a two-dimensional plane formed by the intersection of the x-axis and the y-axis. The point at which the x and y-axis intersect is known as the origin. The coordinate plane can be used to locate points on a plane. The figure below shows five points in a coordinate plane: A, B, C, D, and E.
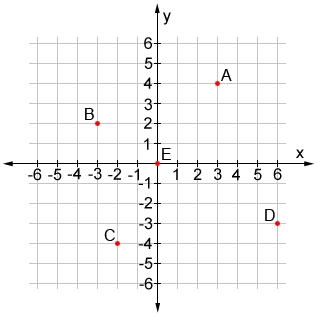
The coordinate plane can also be referred to as the Cartesian coordinate plane, as it is used as part of the Cartesian coordinate system.
Parts of a coordinate plane
Several properties characterize a coordinate plane.
x-axis, y-axis, and origin
A coordinate plane is formed by the intersection of a horizontal number line called the x-axis and a vertical number line called the y-axis. The two axes (plural for axis) intersect vertically at a point called the origin of the coordinate plane.
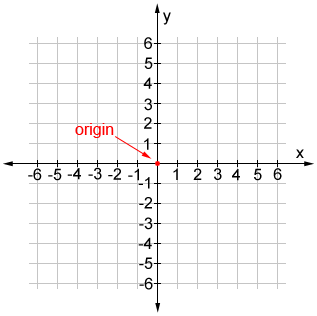
A grid is often drawn on a coordinate plane to make it easier to locate a point. A grid is a set of uniformly spaced horizontal and vertical lines. The grid on the coordinate plane above is shown with light gray line segments.
Ordered pairs and quadrants
The location of a point is given as an ordered pair of numbers, (x1, y1). The first number in the pair is referred to as the x-coordinate. It represents the position of the point on the x-axis. Similarly, the second number represents the position of the point on the y-axis and is accordingly named the y-coordinate.
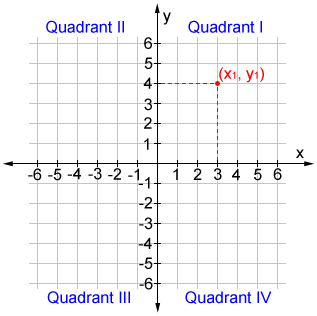
The axes also divide the coordinate plane into four regions called quadrants as shown in the coordinate plane above. Quadrant I is the quadrant in the top right. The numbering of the quadrants proceeds counter-clockwise from quadrant I such that quadrant II is the top left quadrant, quadrant III is the bottom left quadrant, and quadrant IV is the bottom right quadrant. The quadrants can be used to determine the sign of the x and y-coordinates. The sign of the x and y-coordinates in each quadrant does not change. For example, all x-values and all y-values in quadrant I are positive; in quadrant II, all x-values are negative and all y-values are positive; all x-values and all y-values in quadrant III are negative; in quadrant IV, all x-values are positive and all y-values are negative.
Locating a point in the coordinate plane
Start from the origin when locating a point in the coordinate plane. Count in either the positive (right) or negative (left) direction along the x-axis to determine a point's horizontal position. Count in either the positive (up) or negative (down) direction along the y-axis to determine a point's vertical position, as shown in the figure below.
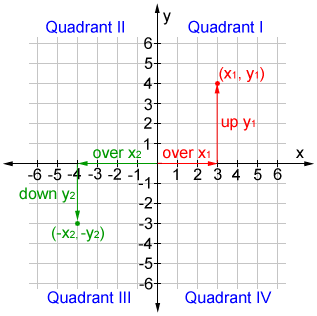
Two points, one in quadrant I and one in quadrant III are shown in the figure above.
Example:
Write the ordered pairs for points A, B, and C shown on the coordinate plane below.
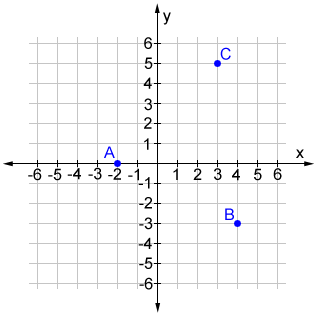
Starting from the origin:
For point A, move to the left 2 units to get an x-coordinate of -2. Since there is no vertical distance to move, the y-coordinate is 0. The ordered pair for point A is (-2, 0).
For point B, move to the right 4 units to get an x-coordinate of 4, then move down 3 units to get a y-coordinate of -3. The ordered pair for point B is (4, -3).
For point C, move to the right 3 units to get an x-coordinate of 3, then move up 5 units to get a y-coordinate of 5. The ordered pair for point C for (3, 5).
Graphing a solution set in the coordinate plane
The graph of an equation written in terms of x and y in the coordinate plane is the set of points (x, y) that represents the solution set of the equation.
For example, three solutions (there are infinitely many) for y = 2x-1 are shown below.
| x | y = 2x - 1 | (x, y) |
|---|---|---|
| -2 | y = 2(-2) - 1 = -5 | (-2, -5) |
| 0 | y = 2(0) - 1 = -1 | (0, -1) |
| 2 | y = 2(2) - 1 = 3 | (2, 3) |
The graph of the solution set is shown in the coordinate plane below.
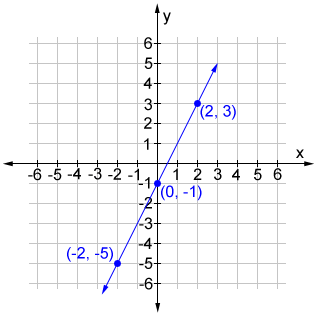
The graph contains the three points determined above. Any point on the graph of the line is part of the solution set for y = 2x - 1. As an example, (3, 5) is another point on the line, and plugging it in yields:
5 = 2(3) - 1
5 = 5 is a true statement, so (3, 5) is a solution for y = 2x - 1.
Did you know?
There are many other coordinate systems used today. One of these is the Global Positioning System (GPS), a system that allows you to find your location anywhere on Earth at any time, regardless of the weather.
