Perpendicular
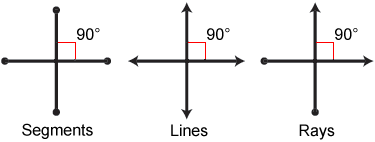
The term "perpendicular" means meeting or crossing at right angles. Lines, rays, line segments, and planes can be perpendicular.
Perpendicular lines, rays, and line segments are lines or parts of lines that meet or cross at right angles.
If lines l and m are perpendicular to each other, we can write l⊥m where "⊥" is the symbol for perpendicular.
Rules involving perpendicular lines
Perpendicular lines create interesting properties and relationships in geometry, the following are some of them:
• A triangle is a right triangle if 2 sides of the triangle are perpendicular.
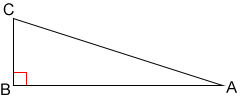
In the diagram above, triangle ABC is a right triangle with right angle at vertex B because sides AB and BC are perpendicular.
• In plane geometry, there can be only one line drawn through a given point not on a given line that is perpendicular to the given line. This is known as the perpendicular postulate.
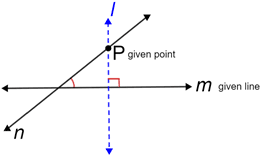
In the diagram above, only line l can be drawn through point P that is perpendicular to line m. Any other line drawn through P, such as line n in the diagram, will not be perpendicular to line m.
• The distance from a point not on a line to the line is the length of the perpendicular line segment from the point to the line. It is also the shortest distance from the point to the line.
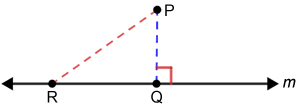
In the diagram above, the distance from P to m is the length of segment since it is perpendicular to m. Notice that segment is also a measurable distance from P to m but not the shortest measurable distance since it is not perpendicular to m.
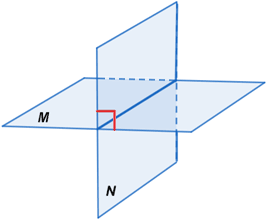
• Two planes that intersect at a right angle are perpendicular to each other.
• A line is called a perpendicular bisector of a line segment if it is perpendicular to the segment and cuts the segment into 2 equal parts.
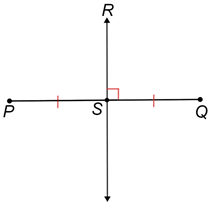
In the diagram above, is the perpendicular bisector of since is perpendicular to and, ≅.
• The altitude of a triangle is the perpendicular line segment from a vertex to the opposite side or the line containing the opposite side of a triangle.
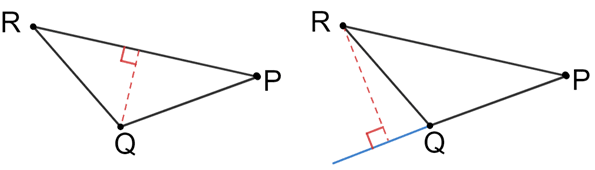
In the diagram above, the dashed segments perpendicular from vertex Q to side PR and from vertex R to side PQ are both altitudes for triangle PQR.
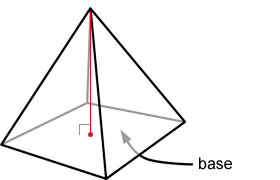
• The height of a pyramid is the perpendicular line segment from the base of the pyramid to its vertex.
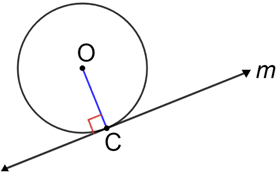
• A line tangent to a circle is perpendicular to the radius of the circle that meets the line at the point of tangency.