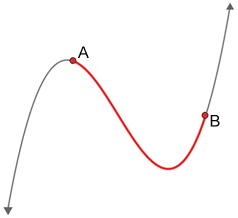
Arc
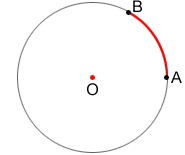
Arcs are often studied in geometry within the context of arcs of a circle. On a circle, you can think of an arc as a part of the circumference of the circle, as shown in the figure below.
Arcs also exist as part of curves, but most of the time, when people refer to an arc, they are usually referring to the arc of a circle rather than that of a curve. Likewise, this page will focus on the topic of arcs of a circle.
, is shown in red above.Arcs are widely used in engineering and other areas of everyday life. The bridge shown below has supports in the shape of an arc.
Types of arcs
A semicircle is the name for an arc that encompasses one-half of a circle's circumference (one meaning of semi- is half).
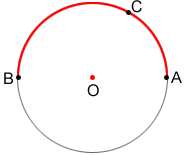
in red is a semicircle for circle O.There are two other types of arcs: minor arcs and major arcs. A minor arc is an arc that has a length that is shorter than that of a semicircle. A major arc has an arc length that is greater than that of a semicircle.
In the figure below, 
is a minor arc. Minor arcs are typically named only by their endpoints. 
is a major arc. Major arcs are named by their endpoints and some other point that lies on the arc.
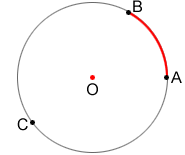
Central angle
A central angle is an angle whose vertex is the center of a circle. When the endpoints of an arc intersect the sides of a central angle, we say the arc subtends the angle. The measure of the arc is equal to the measure of the central angle subtended by the arc.
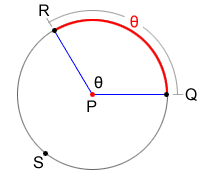
subtends ∠QPR so, the measure of is also θ.Also, since the circumference of a circle is 360°, we can find the measure of the major arc by finding the difference of 360° and the measure of the minor arc. So,
Arc addition
An arc formed by two adjacent arcs has a measure that is the sum of the two adjacent arcs.
Example:
Find 
if 
= 205° for circle O below.
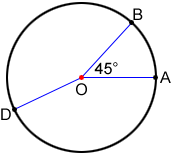
205° = 45° +
= 160°Other angles and arcs
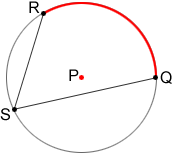
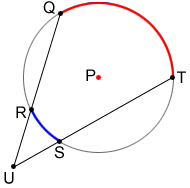
An inscribed angle is the angle formed in the interior of a circle when two chord or secant lines intersect on the circle. ∠RSQ in the figure below is an example. The measure of an inscribed angle is one-half the measure of the angle subtended by the arc. In the figure below,
The measure of each angle formed by two intersecting chords inside a circle is one-half the sum of the arcs that subtend the angles. In the figure below,
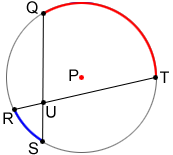
The measure of an angle formed by two secants that intersect outside of a circle is one-half the difference of the arcs that subtend the angle formed by the secants. In the figure below,
Arc length
Since the measure of an arc equals the measure of its central angle, we can determine arc length using the ratio of the arc's central angle to 360°. Given an arc measuring 60°, the ratio would be (60°)/(360°)=1/6. So, the arc makes up 1/6 of the circumference of the circle. Since the length of the circumference of a circle is 2πr, the length of the arc is 
.
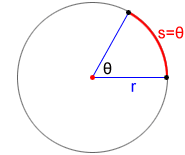
In general, the length of an arc, s, is:
where r is the radius of the circle and θ is the angle in degrees. If the angle θ is in radians, the arc length is:
s = rθ
Example:
Refer to the above figure. Given a circle with a radius of 15 and θ=120°, find the length of arc s.
Other uses of arcs
Arcs are also defined in a Calculus context. An arc is a part of a differentiable curve. One way to think about this without a Calculus background is that in a differentiable curve, the section of the curve doesn't have any breaks in the curve, and that it is smooth and doesn't have any "pointy" sections, like a V, or the absolute value function does.
