Compass
In geometry, a compass is a tool that can be used to draw circles and arcs, as well as to copy line segments. Many plane figures can be constructed with only a compass and a straightedge.
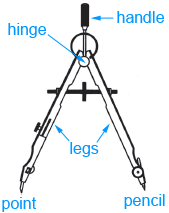
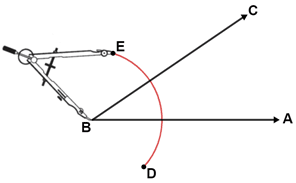
A compass, like the one shown above, has a handle for the user to hold, a hinge that can be opened or closed by moving one or both legs, a point which is stationary or fixed, and a pencil that draws the circle or arc by rotating the pencil leg around the point leg on paper.
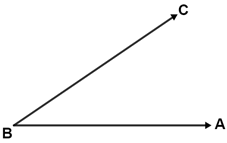
Reconstructing an angle using a compass
An angle, like ∠ABC below, can be reconstructed with a compass and straightedge using the following steps:
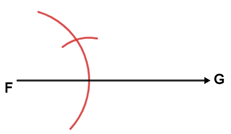
1. Draw ray FG.

2. Placing the compass point on B, open the compass' pencil to a random point, D.
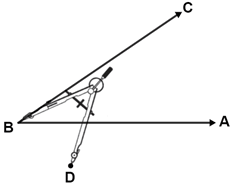
3. Keep the same compass width, BD, and draw arc DE through rays AB and BC.
4. Keeping the same compass width, place the compass point on F and draw an arc through ray FG.

5. Label the intersections of arc DE and angle ABC from step 3, P and Q. Place the compass point on P and the pencil on point Q, then draw an arc through Q.
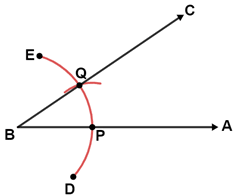
6. Keeping the compass radius the same, place the compass point on the intersection of the arc and ray FG drawn in step 4, then draw an arc. Make sure this arc intersects the arc drawn in step 4.
7. Draw a ray from F through the intersection of the two arcs. Label the head of the ray H.
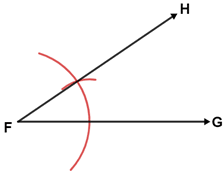
The constructed angle GFH is congruent to the original angle ABC
Navigational compasses
Outside the scope of mathematics, a compass can also refer to a navigational device like the one shown below. It is a tool used for determining direction relative to the geographic cardinal directions.