Sagitta
A sagitta is the height of an arc of a circle. It is a line segment whose endpoints lie on the midpoint of the chord and the midpoint of the arc the chord subtends.
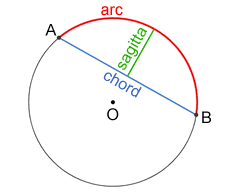
Chord AB subtends arc AB in circle O above. The line segment in green is the sagitta. Since the sagitta links the midpoints of both the arc and chord, the sagitta and chord are perpendicular.
Calculating the sagitta
We can find the length of the sagitta using right triangles.
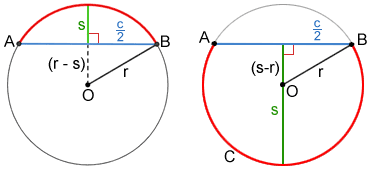
Circle O above has a radius of length r, a sagitta of length s, and a chord of length c. As show above, when a chord and a radius are given, there are two possible arcs involved, a minor arc or a major arc. A minor arc means the arc is less than half of the circle, while a major arc is more than half of the circle.
Chord AB and sagitta s are perpendicular, so they form a right angle at their intersection. This right triangle has hypotenuse r and one side . The other side is either (s-r) or (r-s) depending on if the arc is a minor arc or major arc.
If the length of the radius and chord are given, the following steps can be used to calculate the length of the sagitta.
Similarly, we can find the lengths of the chord and radius using the following equations. These equations work for both minor and major arcs.
Example:
A chord of 4 subtends an arc for a circle with a radius of 3. What is the length of the sagitta?
Since c = 4, and r = 3 we have,
| s = | |
| = | |
| = | |
| = | 0.764 or 5.236 |
Therefore, the length of the sagitta is 0.764 if the arc is a minor arc. The length is 5.236 if it is a major arc.
Did you know?

In order to construct the frame that surrounds the curved portion of the window above, an architect needs to determine relationships certain lengths of the window. The radius of the window, the line segment connecting the ends of the curved window and the distance between the highest point of the curved window and middle of the line segment, called the sagitta, are all critical dimensions in constructing the window's frame.
