Circle formula
A circle is defined as the set of all points equidistant from a fixed point on a plane. There are many circle formulas, such as the area of a circle formula, circumference formula, and diameter formula, all of which are discussed below along with the equations for a circle.
Parts of a circle
The figure below shows the key parts of a circle that we need to know to be able to work with circles and their formulas.

Diameter of a circle formula
The diameter of a circle, is d = 2r, where d is the diameter and r is the radius:
d = 2r
Circumference of a circle formula
The circumference of a circle is C = 2πr. Circumference is a measure of the distance around the circle.

Imagine cutting the circle and straightening it out; the length of the straightened line is the circumference.
There are a few circumference of a circle formulas.
Circumference formula using radius
C = 2πr
where r is the circle's radius and π is a mathematical constant approximately equal to 3.14159.
Circumference formula using diameter
C = πd
where d is the diameter and π is a mathematical constant approximately equal to 3.14159.
Circumference formula using area
where A is area and π is a mathematical constant approximately equal to 3.14159.
Arc length formula
The arc length, s, of a circle is , where θ is the central angle, as shown in the figure below.

Sector formula
The sector of a circle formula is . The sector area is shown in red below:

Area of a circle formula
The area of a circle formula is A = πr2. The area of a circle is the plane region bounded by the circle's circumference. The figure below depicts the area of a circle in red bounded by the circumference in grey.

There are a few area formulas.
Area of a circle using radius
A = πr2
where r is the circle's radius and π is a mathematical constant approximately equal to 3.14159.
Area of a circle using diameter
where d is the diameter and π is a mathematical constant approximately equal to 3.14159.
Area of a circle using circumference
where C is the circumference and π is a mathematical constant approximately equal to 3.14159.
Equation of a circle
In coordinate geometry, a circle can be expressed using different equations and based on various constraints.
Standard equation of a circle
The standard equation of a circle is (x - h)2 + (y - k)2 = r2. This equation can be used for a circle that lies anywhere in the coordinate plane.
Derivation of the standard equation of a circle
The standard equation of a circle is derived using the distance formula. Consider the following figure.
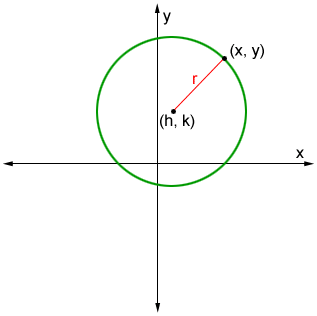
Given a circle with radius, r, centered at point (h, k), we can use the distance formula to find that
where (x, y) is any point on the circle.
Squaring both sides of the equation, yields the standard equation of a circle:
(x - h)2 + (y - k)2 = r2
Example:
Find the equation of the circle with center (4, -3) and radius 5.
Substituting the coordinates of the center and radius we get,
(x - 4)2 + (y -( -3))2 = 52
(x - 4)2 + (y + 3)2 = 25
Notice that if the circle is centered at the origin, (0, 0), then both h and k in the equation above are 0 and the equation reduces to:
x2 + y2 = r2
This is the standard equation of a circle centered about the origin.
Standard equation for a circle centered at the origin
The standard equation of a circle centered about the origin is x2 + y2 = r2. We can see this by plugging (0, 0) in for (h, k) in the standard equation of a circle. We can also derive this equation as follows.
Given that point (x, y) lies on a circle with radius r centered at the origin of the coordinate plane, it forms a right triangle with sides x and y, and hypotenuse r.
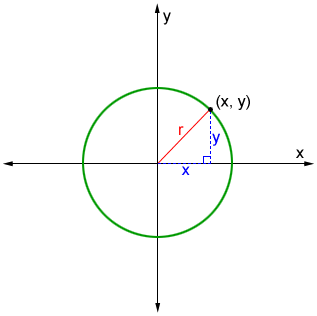
Referencing the figure, we can use the Pythagorean Theorem to find that the equation for this circle in standard form is
x2 + y2 = r2
since any point on the circle is an equal distance, r, from the center.
General form of a circle
The equation of a circle in general form is, x2 + y2 + Dx + Ey + F = 0, where D, E, and F are real numbers.
To more easily identify the center and radius of a circle given in general form, we can convert the equation to standard form.
Example:
Find the center and radius for the circle with equation,
x2 + y2 + 4x - 12y - 9 = 0
Group the x and y terms first.
x2 + 4x + y2 - 12y = 9
Completing the square, we get:
x2 + 4x + 4 + y2 - 12y + 36 = 9 + 4 + 36
(x + 2)2 + (y - 6)2 = 49 = 72
So, the center is (-2, 6) and the radius is 7.
